Can a capacitor increase voltage beyond initial charge?

AI Thread Summary
Charging a capacitor and then separating its plates can indeed result in an increase in voltage beyond the initial charge, due to the decrease in capacitance while maintaining the same charge. This phenomenon is explained by the equation Q = CV, where a reduction in capacitance (C) leads to a higher voltage (V) if the charge (Q) remains constant. However, to achieve a voltage higher than the initial source, the voltage source must be disconnected before the plates are pulled apart. This process is counterintuitive but is rooted in the principles of work and energy in electrical circuits. Understanding this concept is essential for exploring advanced applications of capacitors.
Blackhawk4560
Messages
19
Reaction score
0
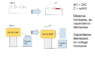
Question: If you charge a capacitor circuit and then separate the capacitor, does voltage increase beyond the initial source?

It seams counter intuitive that if you plug a 9 Volt battery into two metal plates and pull the plates apart that you'll get massive voltage spikes, but that's what the equations seem to point to...

You'll see a diagram of this attached,
Thanks for your time!
 

Attachments

  • Voltage Change.png
    Voltage Change.png
    19.4 KB · Views: 572
Physics news on Phys.org
Blackhawk4560 said:
t seams counter intuitive that if you plug a 9 Volt battery into two metal plates and pull the plates apart
Why counter-intuitive ? You yourself already write you need to pull (i.e. do work) the plates apart.

The capacitance decreases, so, in accordance with Q = CV the voltage must increase if the charge remains the same.

By the way, the guy's name is 'van de Graaff'
 
Ohhhhhhhh I hadn't thought of that work being done... makes sense!

Can that lead to the voltage being HIGHER than the initial source? Or does it cap off at the voltage of the battery/van de GraAff?

Thanks again, blown away by that response time by the way!
 
Blackhawk4560 said:
Can that lead to the voltage being HIGHER than the initial source
Yes. Of course, you first have to disconnect the voltage source before starting to pull on the plates.
 
Thread 'Motional EMF in Faraday disc, co-rotating magnet axial mean flux'

Thread 'Motional EMF in Faraday disc, co-rotating magnet axial mean flux'

So here is the motional EMF formula. Now I understand the standard Faraday paradox that an axis symmetric field source (like a speaker motor ring magnet) has a magnetic field that is frame invariant under rotation around axis of symmetry. The field is static whether you rotate the magnet or not. So far so good. What puzzles me is this , there is a term average magnetic flux or "azimuthal mean" , this term describes the average magnetic field through the area swept by the rotating Faraday...
View full post »

Similar threads

B Some Questions about Electric Current/Capacitors to help my understanding
Replies
7
Views
2K
Van de Graaff help
Replies
5
Views
2K
Confused about electrostatic voltage and DC voltage
Replies
1
Views
1K
Series capacitors and the amounts of charge on the plates.
Replies
22
Views
5K
Let current from a Van de Graff generator flow through you
Replies
5
Views
4K
Potential Energy and Force Between Capacitor Plates
Replies
6
Views
3K
Can You Charge a Polarized Capacitor with a Van de Graaff Generator?
Replies
2
Views
6K
Where does charge go in this van de Graaff generator?
Replies
4
Views
6K
Understanding capacitor behaviour (fully )
Replies
20
Views
10K
Troubleshooting a homemade Van de Graaff machine
Replies
20
Views
4K

Hot Threads

Recent Insights

Back
Top