Can anyone make a differential equation from the below eg:

[abhijath]

[ NOTE ] Thread moved to homework forums by mentor

suppose in a dark room a candle is burning, so darkness increases as we move away from the candle. from the below diagram can anyone derive a differential example to show the rate of change of darkness from candle to point B.

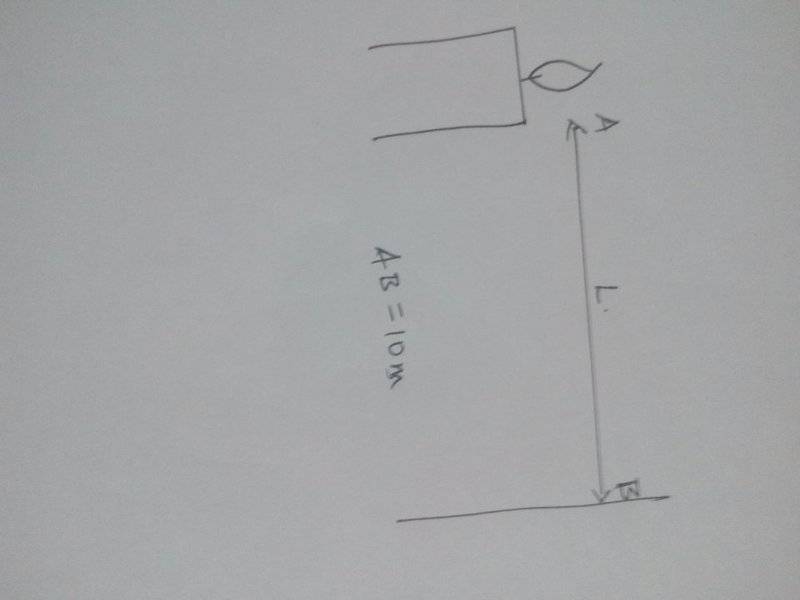
supposing darkness decreases by one unit for every meter and AB is 10 meter.

 

[jedishrfu]

What do you know about the light intensity at some point from the light source?

 

[abhijath]

Take light intensity as 10 at point A

 

[haruspex]

Take light intensity as 10 at point A

jedishrfu means at some arbitrary point at a given distance from the source.

 

[abhijath]

It decreases by 1 unit for every metre from A to B

 

[abhijath]

So light intensity will be zero at point B

 

[haruspex]

supposing darkness decreases by one unit for every meter and AB is 10 meter

First, you don't mean that. Brightness will decrease from A to B.
And "darkness" is not a measurable, brightness is.
But is this statement part of the problem as given to you? Word for word? It's very strange because brightness will not change linearly with distance.

So light intensity will be zero at point B

Again, that doesn't fit with reality.

 

[abhijath]

Forget about reality, Iam just giving a concept so that someone can tell me how is differential equation useful in practical cases.

 

[rude man]

In any case, a diff. eq. is not relevant unless you consider an algebraic equation a diff. eq. of zero order:
brightness = 10(1 - x/10), x in meters.
Of course, this assumption is nonsense as others here have pointed out.

 

[haruspex]

Forget about reality, Iam just giving a concept so that someone can tell me how is differential equation useful in practical cases.

Ok, but your example is not going to demonstrate differential equations being useful. In your example, you can just write down the algebraic relationship of brightness to distance from the given information. (As rudeman has done.). You could then differentiate it to obtain a differential equation, but this doesn't demonstrate any usefulness because you already know the solution.
You would need an example in which the equations you write down initially involve rates of change. Try an object falling, subject to drag which varies as either v or v².