- #1
csmallw
- 25
- 0
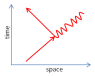
In a metal, can one electron decay into one lower-energy electron plus one phonon? (i.e., can the attached Feynman diagram occur?)
If we replace phonons by photons and consider the process in a vacuum, I guess this is prohibited because you can always boost to a frame where the incoming and outgoing electron velocities are the same. Thus, the electron has no ability to transfer energy to the photon because there are no photons with finite q but zero energy.
However, in a metal, Galilean and Lorentz invariance are broken by the crystal lattice, so it seems to me that the process ought to be allowed. Is my thinking here correct?
If we replace phonons by photons and consider the process in a vacuum, I guess this is prohibited because you can always boost to a frame where the incoming and outgoing electron velocities are the same. Thus, the electron has no ability to transfer energy to the photon because there are no photons with finite q but zero energy.
However, in a metal, Galilean and Lorentz invariance are broken by the crystal lattice, so it seems to me that the process ought to be allowed. Is my thinking here correct?