emhelp100
- 14
- 0
Homework Statement
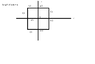
A point charge +Q exists at the origin. Find \oint \vec{E} \cdot \vec{dl} around a square centered around the origin. I know the answer is 0, but can someone check my setup?
Homework Equations
E=\frac{Q(\vec{R}-\vec{R'})}{4\pi E_0 |\vec{R}-\vec{R'}|^3}
The Attempt at a Solution
For E1 and E3, R = \hat{x}x+\hat{y}\frac{a}{2} and R' = 0
E1 = E3 = \frac{Q\hat{x}x+\hat{y}\frac{a}{2}}{4\pi E_0(x^2+\frac{a^2}{4})^{3/2}}
dl1=dl3 = \hat{x}dx
E2=E4=\frac{Q\hat{x}\frac{a}{2}+\hat{y}y}{4\pi E_0(y^2+\frac{a^2}{4})^{3/2}}
dl2=dl4 = \hat{y}dy