doublea500
- 20
- 0
Need help finding Current on one resistor when there are 2 batteries
Find Current in the 3 ohm resistor
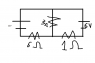
Sorry it didnt come out right. ill explain what it is. 12V meter on the left, + on top - on bottom. then if you go counter-clockwise you will hit a 6ohm resistor, keep going and you will hit a 1 ohm resistor. on the right there's a 6v +top - bottom. in the middle between the 6ohm and 1 ohm there's a 3 ohm separating it comming out.
Imma take a picture
V=IR... and others
I Tried using kirchhoffs law and i kinda got lost. i was trying to do the 2 boxes seperately like 3I+6I=12V so I1=12/9 (1.3333) and 3I+1I=6V so 41=6v so I2=6/4. (1.5). i got stuck there because i didnt know what to do next
The answer for this is 1.8
can someone answer how to do this and tell me the basic rules when there are 2 voltmeters? because the 2 voltmeters really confuses me.
Homework Statement
Find Current in the 3 ohm resistor
Sorry it didnt come out right. ill explain what it is. 12V meter on the left, + on top - on bottom. then if you go counter-clockwise you will hit a 6ohm resistor, keep going and you will hit a 1 ohm resistor. on the right there's a 6v +top - bottom. in the middle between the 6ohm and 1 ohm there's a 3 ohm separating it comming out.
Imma take a picture
Homework Equations
V=IR... and others
The Attempt at a Solution
I Tried using kirchhoffs law and i kinda got lost. i was trying to do the 2 boxes seperately like 3I+6I=12V so I1=12/9 (1.3333) and 3I+1I=6V so 41=6v so I2=6/4. (1.5). i got stuck there because i didnt know what to do next
The answer for this is 1.8
can someone answer how to do this and tell me the basic rules when there are 2 voltmeters? because the 2 voltmeters really confuses me.
Attachments
Last edited: