SUMMARY
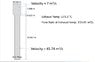
The discussion centers on calculating the velocity at the stack tip for a system with a larger diameter of 2.5 m. The equation V1A1 = V2A2 is initially considered, but participants clarify that this formula is applicable only to incompressible fluids, while flue gases are compressible. The correct interpretation of units is emphasized, with velocities needing to be in m/s rather than m3/s. The final calculated velocity at the stack tip is determined to be 17.82 m/s.
PREREQUISITES
- Understanding of fluid dynamics principles, specifically the continuity equation.
- Familiarity with compressible versus incompressible fluid behavior.
- Knowledge of unit conversions, particularly between volumetric flow rates and velocities.
- Basic grasp of gas laws applicable to flue gases.
NEXT STEPS
- Study the continuity equation in fluid dynamics for both compressible and incompressible fluids.
- Learn about the ideal gas law and its application to flue gases.
- Research the effects of temperature and pressure on gas density and velocity calculations.
- Explore advanced fluid dynamics topics, such as Bernoulli's equation for compressible flows.
USEFUL FOR
Engineers, physicists, and students involved in fluid dynamics, particularly those working with gas flow in industrial applications or HVAC systems.