blake2
- 3
- 0
Ok so I was sitting out back one day listening to some music with some friends around.
We had some music playing on a stereo inside the house and we were out the back with the glass door open about 10 cm's.
I thought I noticed that some sounds with different frequencies seemed louder then other sounds with noticably different frequencies. So i suggested that perhaps the wavelength of some of the sounds with frequency x, was making it through the small gap whereas another sound at the same instance with wavelength and frequency y was not making it through the small gap.
Is this correct?
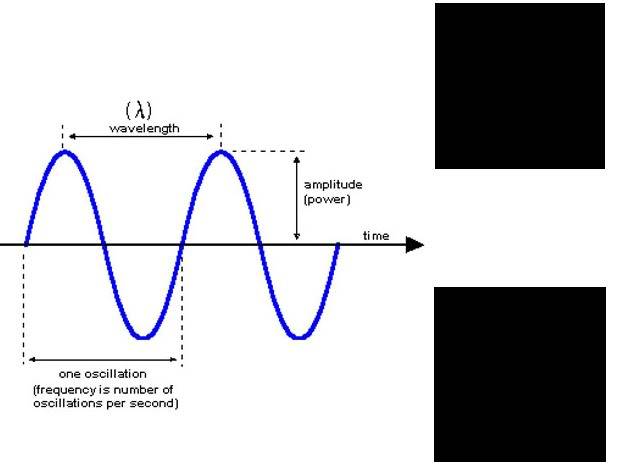
It sounded correct but the more i think about it the more complex it becomes. I cannot imagine a sound wave propagating through 3-dimensional area and where the amplitude comes into effect. I understand how a soundwave is simply compression of air and the distance between two compressions is the wavelength BUT where is the amplitude?
Would a gap smaller then the wavelength effect the intensity of the sound you are hearing or since the wavelength travels longitudinally then the gap would not effect it?
What about amplitude. If the amplitude is of a greater distance then the gap then would the resultant intensity become lesser then a sound with smaller amplitude then the gap?
Ignoring any sound coming through the barriers of course and think theoretically.
You could set up an experiment to emit sounds of differing frequency and amplitude to try and see if the gap effects the resultant intensity of the sound (if a soundwave travel through the gap un-hindered then it is going to be louder then a soundwave that hits the barrier and travels through that)
Its a slit experiment but in 3-dimensions;
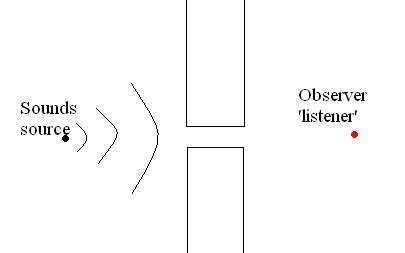
We had some music playing on a stereo inside the house and we were out the back with the glass door open about 10 cm's.
I thought I noticed that some sounds with different frequencies seemed louder then other sounds with noticably different frequencies. So i suggested that perhaps the wavelength of some of the sounds with frequency x, was making it through the small gap whereas another sound at the same instance with wavelength and frequency y was not making it through the small gap.
Is this correct?
It sounded correct but the more i think about it the more complex it becomes. I cannot imagine a sound wave propagating through 3-dimensional area and where the amplitude comes into effect. I understand how a soundwave is simply compression of air and the distance between two compressions is the wavelength BUT where is the amplitude?
Would a gap smaller then the wavelength effect the intensity of the sound you are hearing or since the wavelength travels longitudinally then the gap would not effect it?
What about amplitude. If the amplitude is of a greater distance then the gap then would the resultant intensity become lesser then a sound with smaller amplitude then the gap?
Ignoring any sound coming through the barriers of course and think theoretically.
You could set up an experiment to emit sounds of differing frequency and amplitude to try and see if the gap effects the resultant intensity of the sound (if a soundwave travel through the gap un-hindered then it is going to be louder then a soundwave that hits the barrier and travels through that)
Its a slit experiment but in 3-dimensions;