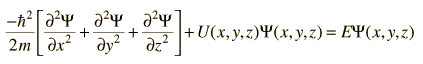Can the Schrödinger Equation be Extended to Four Dimensions?

[moriheru]

This is a rather naive question concerning the dimension of the schrodinger equation. If the Schrodinger equation can be wrtiten in a three dimensional form using the laplacian operator can it be written in a 4d version. I understand that the schrodinger equation shows the development of the state of a particle in time... as I said naive!

 

[Orodruin]

The answer you are looking for would depend on what you consider your four dimensions to be. Is it the space-time of special relativity? Four spatial dimensions? (Say, four particles moving in 1 dimension) Something completely different?

 

[moriheru]

I meant a wave something along the lines of psi(x,y,z,t). Would that give me the evolution of the particles state in a 5 dimensional system?

 

[jtbell]

Do you mean the time-dependent Schrödinger equation (TDSE)?
$$-\frac{\hbar^2}{2m} \left( \frac{\partial^2 \Psi}{\partial x^2} + \frac{\partial^2 \Psi}{\partial y^2} + \frac{\partial^2 \Psi}{\partial z^2} \right) \Psi(x,y,z,t) + U(x,y,z,t) \Psi(x,y,z,t) = i \hbar \frac {\partial}{\partial t} \Psi(x,y,z,t)$$

When V is independent of t, that is, U(x,y,z,t) = U(x,y,z), the solutions of the TDSE are of the form $\psi(x,y,z)e^{-iEt/\hbar}$, where $\psi(x,y,z)$ satisfies the time-independent Schrödinger equation (TISE), which you gave in your first post.

 

[moriheru]

Yep...I mean can one expand the laplacian operator so that one has the deriviativ of x,y,z,t?

 

[Orodruin]

The Klein-Gordon equation $(\partial_t^2 - \nabla^2)\phi = 0$ appears in relativistic quantum mechanics and involves the d'Alembert operator - which in some sense is the relativistic equivalent of the Laplace operator. However, note the difference in sign between the tempotal and spatial derivatives.

In the non-relativistic limit, the KG equation gives back the Schrödinger behaviour.

 

[moriheru]

Something like this?

(d^2/dt^2+d^2/dx+d^2/dy^2+d^2/dz^2)-(h/2pi)/2m psi(x,y,z,t)+V(x,y,z,t)psi(x,y,z,t)=?

instead of