Karol
- 1,380
- 22
Homework Statement
Homework Equations
Maxima/minima are where the first derivative is 0
The Attempt at a Solution
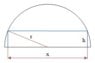
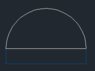
$$r^2=\frac{x^2}{4}+h^2~\rightarrow~h^2=r^2=\frac{x^2}{4}$$
S will be the strength of the light through the whole opening: the semicircle and the rectangle inside.
I take the strength of light through of light through the rectangle as 1 and through the colored glass as ##~\frac{1}{2}##.
$$S=\frac{1}{2}(\text{area of a semicircle})+\frac{1}{2}hx$$
$$S=\frac{1}{2}\left[ \frac{\pi r^2}{2}+hx \right],~~S'=\frac{1}{2}\left[ \left( -\frac{2x}{4} \right)x+h \right]$$
$$S=\frac{1}{2}\left[ \left( r^2-\frac{x^2}{4} \right)-\frac{x^2}{2} \right],~~S'=0:~~\rightarrow~~x^2=-4r^2$$
If i try the ##~GM \leq AM~##: ##~\sqrt{h^2x^2}\leq \frac{h^2+x^2}{2}##
In order to maximize the left side equality is when the elements are equal: ##~x^2=h^2~\rightarrow~x^2=h^2-\frac{x^2}{4}~\rightarrow~x^2=\frac{4r^2}{5}##
Both answers are wrong
 ).
).