Homgkung
- 5
- 4
- Homework Statement
- finding the angular acceleration by using newton's second law for a system of particles
- Relevant Equations
- torque = I a
F=ma
Summary: When I tried to find the angular frequency of a rod pendulum, I attempted to find its angular acceleration first, however, I realized that the results are different by using different approaches. i.e. (1) Newton's second law for a system of particles (2) Newton's second law for rotation.
The two approaches should give the same angular acceleration.
can anyone check if any mistakes in my first approach? Much appreciated!
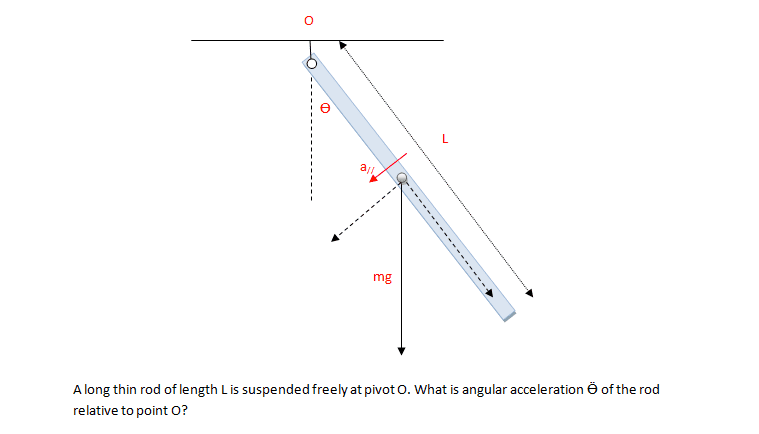
Approach 1
Take the whole rod as a system, so we can apply Newton's Second Law for a system of particles.
The Newton's Second Law for a system of particles states that the total net force equals the mass of the rod multiplies the acceleration of the center of mass (or CG here), which is located at the center of the rod.
As the CG moves along a circular path, we can resolve the acceleration of the CG into the radial component and the tangential component a//.
As we are just interested in the angular accelerated, we just consider the tangential motion.
a// = (L/2)Ӫ (1)
where Ӫ is the angular acceleration of the rod
Then we can also resolve the gravity in the radial component and tangential component (-mg *sinϴ). By using Newton's second law for a system of particles, the tangential acceleration is determined solely by the tangential component of the gravity, which means
-mg*(sinϴ) = m*a// (2)
(the radial acceleration is determined by the Reaction force from the pivot and the radial component of the gravity, however, the radial acceleration does not affect the angular acceleration, so we could ignore it here.)
(1) and (2) give:
Ӫ = -(2/L)g* sinϴ (*)
Approach 2
By using Newton's second law for rotation, we can easily apply the following relationship
τ = I Ӫ (3)
, where τ is the torque about point O and I is the moment of inertia, which equals 1/3 m L^2 .
The net torque is just the torque of the gravity, τ = -L/2*mg* sinϴ (4)
Linking (3) and (4) , we have
Ӫ = -(3/2L) g* sinϴ (**)
Conclusion:
The angular acceleration from approach 1 and 2 are so different!
Questions
I am pretty sure that the (**) is correct while (*) is not, however, I couldn't find any problems in the working in approach 1 (which bothers me so much).
Please help to identify the mistake(s) I made in approach 1 ! much appreciated!
The two approaches should give the same angular acceleration.
can anyone check if any mistakes in my first approach? Much appreciated!
Approach 1
Take the whole rod as a system, so we can apply Newton's Second Law for a system of particles.
The Newton's Second Law for a system of particles states that the total net force equals the mass of the rod multiplies the acceleration of the center of mass (or CG here), which is located at the center of the rod.
As the CG moves along a circular path, we can resolve the acceleration of the CG into the radial component and the tangential component a//.
As we are just interested in the angular accelerated, we just consider the tangential motion.
a// = (L/2)Ӫ (1)
where Ӫ is the angular acceleration of the rod
Then we can also resolve the gravity in the radial component and tangential component (-mg *sinϴ). By using Newton's second law for a system of particles, the tangential acceleration is determined solely by the tangential component of the gravity, which means
-mg*(sinϴ) = m*a// (2)
(the radial acceleration is determined by the Reaction force from the pivot and the radial component of the gravity, however, the radial acceleration does not affect the angular acceleration, so we could ignore it here.)
(1) and (2) give:
Ӫ = -(2/L)g* sinϴ (*)
Approach 2
By using Newton's second law for rotation, we can easily apply the following relationship
τ = I Ӫ (3)
, where τ is the torque about point O and I is the moment of inertia, which equals 1/3 m L^2 .
The net torque is just the torque of the gravity, τ = -L/2*mg* sinϴ (4)
Linking (3) and (4) , we have
Ӫ = -(3/2L) g* sinϴ (**)
Conclusion:
The angular acceleration from approach 1 and 2 are so different!
Questions
I am pretty sure that the (**) is correct while (*) is not, however, I couldn't find any problems in the working in approach 1 (which bothers me so much).
Please help to identify the mistake(s) I made in approach 1 ! much appreciated!
Attachments
Last edited:
