You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Can you solve this challenging integral using a clever modification?
Physics news on Phys.org
mfb
Mentor
- 37,373
- 14,204
Expanding with ##\sqrt{\ln(9-x)}-\sqrt{\ln(3+x)}## gives
$$\frac {\sqrt{\ln(9-x)}\left(\sqrt{\ln(9-x)}-\sqrt{\ln(3+x)}\right)} {\ln(9-x)-\ln(3+x)}$$
That can be split into two parts, where one part looks easy and the other part can be simplified significantly. I don't know if that will lead to a solution, however.
$$\frac {\sqrt{\ln(9-x)}\left(\sqrt{\ln(9-x)}-\sqrt{\ln(3+x)}\right)} {\ln(9-x)-\ln(3+x)}$$
That can be split into two parts, where one part looks easy and the other part can be simplified significantly. I don't know if that will lead to a solution, however.
omri_mar
- 17
- 2
first of all thank you!
Ive tried this and it lead me nowhere..
Ive tried this and it lead me nowhere..
mfb
Mentor
- 37,373
- 14,204
Hmm okay, I don't see how to solve the remaining part either.
An interesting observation: 3+x goes from 5 to 7, while 9-x goes from 7 to 5. There could be some symmetry to exploit, but I did not find it yet.
An interesting observation: 3+x goes from 5 to 7, while 9-x goes from 7 to 5. There could be some symmetry to exploit, but I did not find it yet.
omri_mar
- 17
- 2
Thats actually very interesting because according to the answers the answer is 1.
Can someone help me...?
Can someone help me...?
Curious3141
Homework Helper
- 2,861
- 89
Hint: substitute ##\displaystyle x = 6-y##.
EDIT: numerous glitches in the PF software are making it difficult to post. Basically, I wanted to add: don't try to simplify the integrand, etc. Just do the sub, and see what happens to the bounds. This is actually a very simple problem in disguise.
EDIT: numerous glitches in the PF software are making it difficult to post. Basically, I wanted to add: don't try to simplify the integrand, etc. Just do the sub, and see what happens to the bounds. This is actually a very simple problem in disguise.
Last edited:
omri_mar
- 17
- 2
I can't remove the disguise... :(
mfb
Mentor
- 37,373
- 14,204
Ah nice, that is the right way to solve it.
@omri_mar: You can modify this new integrand to look similar to the old one now.
@omri_mar: You can modify this new integrand to look similar to the old one now.
omri_mar
- 17
- 2
I don't get it. How can I continue?
cpt_carrot
- 29
- 4
Try adding together the new integral and the old one
omri_mar
- 17
- 2
what do you mean?
mfb
Mentor
- 37,373
- 14,204
You have an equation (old integral)=(new integral). Try to write (new integral) as (something)-(old integral). This gives you an equation like 2*(old integral)=(something), and (something) is easy to calculate.
Don't write PMs, please.
Don't write PMs, please.
Curious3141
Homework Helper
- 2,861
- 89
omri_mar said:this is what i get
Sorry for the late reply - I just noticed your bounds are off in the attachment to post 8. Your bounds should be reversed (identical to the original integral). Don't forget that ##dy = -dx##. Other than that, the other posters have already told you how to proceed. Remember that in a definite integral, the variable of integration is basically just a dummy variable, so whether it's x or y, it doesn't matter. So just replace the y in the new integral with x, and add it to the original integral. Now you have twice the original integral, and it's equal to something very simple.
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
(Most of post deleted in Edit. It was pretty much redundant with Curious3141 post. )omri_mar said:this is what i get
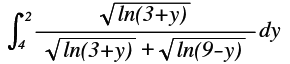
Now modify the numerator by adding and subtracting ... (something clever) .
Last edited:
Similar threads
- Replies
- 9
- Views
- 2K
- Replies
- 22
- Views
- 2K
- Replies
- 4
- Views
- 1K
- Replies
- 2
- Views
- 969
- Replies
- 4
- Views
- 1K
- Replies
- 6
- Views
- 2K
- Replies
- 8
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 2
- Views
- 2K
- Replies
- 9
- Views
- 3K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 96
- Calculus and Beyond Homework Help
-
Solving the wave equation with piecewise initial conditions
- Started by songoku
- Replies: 11
- Calculus and Beyond Homework Help
-
Area of loop in x-y plane
- Started by littlemathquark
- Replies: 20
- Calculus and Beyond Homework Help
-
Solve this problem that involves induction
- Started by chwala
- Replies: 7
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math