Cannon shooting emergency packets

[naianator]

Homework Statement

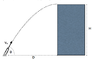
A cannon at ground level is shooting emergency packets to people stranded on the roof of a flooded building of height H=120 meters. The corner of the building is located a distance D=40 meters from the cannon. It is desired that the incoming packets are flying tangent to the roof as shown so that they land gently with as little impact as possible and slide along to a stop.

Find the initial speed v0 and at what angle θ (in degrees) the cannon should be aimed to achieve the above scenario.

Homework Equations

x(t)=x_0+v_0x*t+1/2*a*t^2

The Attempt at a Solution

x(t)=v_ox*t
40=v_ox*t
t=40/v_ox
y(t)=v_oy*t-1/2*g*t^2
120=v_oy*t-1/2*g*t^2
v_y(t)=v_oy-g*t and since it hits the roof at the top of the curve v_y(t)=0=v_oy-g*t and
t=v_oy/g
This is where I get stuck. v_oy/g=40/v_ox and i can't find a way to relate the velocities so that i can substitute tan(theta)=v_oy/v_ox

Same goes if i try to substitute t=40/v_ox into 120=v_oy*t-1/2*g*t^2 so maybe I'm just going about this the wrong way

Please help

 

[phinds]

... tangent to the roof as shown ...

Shown where?

 

[haruspex]

You have three equations and three unknowns. The basic technique is to find or develop an equation which expresses one unknown in terms of the other two, then use this to replace that unknown in each of the other two equations. You will then have two equations with two unknowns. Repeat process.

 

[naianator]

You have three equations and three unknowns. The basic technique is to find or develop an equation which expresses one unknown in terms of the other two, then use this to replace that unknown in each of the other two equations. You will then have two equations with two unknowns. Repeat process.

Thats sort of what I've been trying to do. Any suggestions as to which one to use?

 

[naianator]

i found v_ox=40/t so v_ox=40g/v_oy and v_oy=v_ox*tan(theta) so v_ox=sqrt(40g/tan(theta)) but I'm not sure how to relate that back to v or if it even helps me

and i think the picture should be attached now

 

[haruspex]

Thats sort of what I've been trying to do. Any suggestions as to which one to use?

You had v_oy/g=40/v_ox, and you mentioned substituting t=40/v_ox into 120=v_oy*t-1/2*g*t^2, but didn't post the result.
Having made those two steps, you should be down to two equations and two unknowns.

 

[naianator]

You had v_oy/g=40/v_ox, and you mentioned substituting t=40/v_ox into 120=v_oy*t-1/2*g*t^2, but didn't post the result.
Having made those two steps, you should be down to two equations and two unknowns.

Yes, I got it thank you. I was overlooking a couple of things.