zippeh
- 12
- 0
Homework Statement
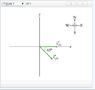
A canoe has a velocity of 0.360m/s southeast (at 315°) relative to the earth. The canoe is on a river that is flowing at 0.580m/s east relative to the earth.
Find the magnitude of the velocity v⃗ c/r of the canoe relative to the river.
Homework Equations
Vx=V0cos(θ)
Vy=V0sin(θ)
The Attempt at a Solution
The answer is Vc/r=0.413 m/s and the (Vc/r)x , (Vc/r)y =
-0.325,-0.255 ; respectively.
There are a few things I am confused about with the equations on the problem in general. Firstly, why do these equations work : Vx=V0cos(θ) and Vy=V0sin(θ).
I don't understand why I have to use these equations in the problem to obtain the Vx when the problem (to my understanding) gives me Vx and the Vy, which should be the value of Vc/r since this should be just simple vector addition. This is what I am thinking (see attachments). The magnitude of the velocity of Vc/r = Vc/e - Vr/e. So, Vc/e is given at a 315° angle at a velocity of .350m/s. Then using the head to tail method, -Vr/e is given at 180° at a velocity of .580m/s. Using the cos(315°)*.360, I should get -.255 for the magnitude of the velocity of Vc/r instead of .413. I know this is obviously wrong since you can't have a negative velocity in this problem, the way they have the positive and negative planes set up, but I just want to know why the other way works and why it isn't simple vector addition/subtraction. Thanks in advance!