Capacititive Circuit - discharging through lamp and resistor

[CAF123]

Homework Statement

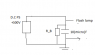
The power supply for a large flash lamp is shown below where a 500 V DC power supply changes up at 10 μF capacitor that then discharged through the flash lamp.

Such a system is potenitally lethal, so to reduce risk a bleed resistor Rb is connect across the capacitor to discharge it when the DC power supply is disconnected. The safety specification is that the capacitor should be reduced to a safe voltage (30 V), 15 second after the DC power supply is disconnected. Calculate,

1. the required value of Rb,
2. the maximum power dissapated in Rb when the system when(??) the DC power supply is connected.(disconnected?)

The Attempt at a Solution

1) I think this is just a use of the equation $$V(t) = V_o exp\left(-\frac{t}{RC}\right),$$with V = 30, V₀ = 500, t = 15 and C = 10μF and then solve for R.

2) I don't really understand the question, particularly because I don't understand the english used. What I have though is that $P_R(t) =$power dissipated in the resistor = $I_R(t) V_R(t) = I_2^R(t) V_R(t).$ Should I first find the time it takes for the capacitor to charge up to 500V. I am presuming that the 'connected' there should be 'disconnected'.

Many thanks.

 

[NascentOxygen]

I'd say it is not meant to be complicated. The resistor is consuming (and wasting) power while the 500V supply is connected. How much power is the resistor dissipating?

Does the book give the correct answer?

 

[voko]

Connected really means connected. Note that when the capacitor is fully charged, its resistance is essentially infinite, so you can ignore it (and the flash lamp). What does the circuit reduce to in this case? What current flows through it?

 

[CAF123]

I'd say it is not meant to be complicated. The resistor is consuming (and wasting) power while the 500V supply is connected. How much power is the resistor dissipating?

Does the book give the correct answer?

I thought it may have been simple too, but then I reliased that everything is a function of t, so I am not sure if straight application of Ohm's Law here would work. In the case that I am mistaken, what I said was: If $V_o = 500V, R_B = 5.3 \times 10^5 Ω, ($from 1)) then$I = V_o/R_B$. So then $P_R = V_o^2/R_B$. Right?

If this is right, could you explain why it is valid given what I said above about time dependent functions of V,I?

I do not have access to the correct answer for this question.

 

[CAF123]

Connected really means connected.

Ok thanks. I wasn't sure since as you can probably tell from the rest of the question, the grammer/spelling is all over the place.(I copied and pasted the question from another source and somehow I forgot to edit the mistakes).

Note that when the capacitor is fully charged, its resistance is essentially infinite,

Why is this so?

so you can ignore it (and the flash lamp). What does the circuit reduce to in this case? What current flows through it?

If the resistance is essentially infinite, then the current would tend to zero.

 

[voko]

Why is this so?

When a capacitor is fully charged, no current can flow through it.

If the resistance is essentially infinite, then the current would tend to zero.

Through the capacitor - yes. But the resistor is in parallel.

 

[CAF123]

Through the capacitor - yes. But the resistor is in parallel.

So all the current goes through the resistor.

 

[voko]

So all the current goes through the resistor.

Indeed.

 

[CAF123]

Indeed.

So what I did in post #4 is correct then? At the moment the supply is connected we have $V_0 = 500V$ and this tails away exponentially. Using the value of $R_B$ deduced in 1), I can then find the current, which then allows me to find power.

I presume this is correct because I am looking for the power dissipated the moment the supply is connected and so provided the supply is still connected, V does not change, the current is exclusively through the resistor and I assume that the resistance of the bleed resistor is constant, yes?

 

[NascentOxygen]

So what I did in post #4 is correct then? At the moment the supply is connected we have $V_0 = 500V$ and this tails away exponentially.

The voltage from the power supply does not tail away, it stays fixed at 500V. (Sure, when the lamp is fired the resistor voltage changes, but this is a minor blip and not taken into account when determining the power that that resistor continuously wastes when powered by 500V.)

The application is one where the lamp is fired only now and then; most of the time the lamp circuit is standing by in a state of readiness, with the cap fully charged.

 

[CAF123]

Sorry, NascentOxygen, I meant that when the supply is disconnected, V drops exponentially.

 

[NascentOxygen]

Sorry, NascentOxygen, I meant that when the supply is disconnected, V drops exponentially.

That happens at the end of the day when you switch the gear off before going home.

 

[CAF123]

That happens at the end of the day when you switch the gear off before going home.

I am not sure I understand. The question says the power supply is disconnected and 15s later, we want the voltage across the capacitor to be 30V?

 

[voko]

The question is about the dissipated power "when the system when the DC power supply is connected."

 

[NascentOxygen]

I am not sure I understand. The question says the power supply is disconnected and 15s later, we want the voltage across the capacitor to be 30V?

It's a common safety technique. The resistor is not required for the apparatus to function in its intended role. The resistor is there to drain the lethal charge from the capacitor as a safeguard for any unsuspecting person who attempts to repair or modify the apparatus.

Just because equipment is switched off, and unplugged from the mains, does not make it safe to work on, though we too often forget this. The resistor is incorporated in the circuit to render the inner workings safe for probing fingers (and meter probes) of even the incautious repairer.

Nevertheless, before working on such elements, you should always discharge large caps yourself, just in case the resistor connection is broken.

 

[CAF123]

The question is about the dissipated power "when the system when the DC power supply is connected."

Yes, that is part 2). So I take V = 500 there. But in the first part, we are considering the case where the power supply is no longer connected, so V tails off exponentially, right? To get the capacitor to 30V in 15s after the supply is disconnected, we require the 'bleed' resistor to have the right resistance such that the voltage is 30V after 15s.

 

[voko]

In the first part, the power supply is disconnected and the capacitor fully charged, and you have to find the resistance meeting certain requirements. Voltage falls off exponentially.

Then, when you have the resistance, you are to consider what happens when the power supply is connected, specifically how much power is wasted. Voltage is constant.

 

[CAF123]

In the first part, the power supply is disconnected and the capacitor fully charged, and you have to find the resistance meeting certain requirements. Voltage falls off exponentially.

Then, when you have the resistance, you are to consider what happens when the power supply is connected, specifically how much power is wasted. Voltage is constant.

This makes sense. I believed I have outlined my approach to this in the earlier posts. Does it look good?

Many thanks.

 

[voko]

I think at this stage you should be able to plug in the numbers and get the results.

 

[CAF123]

So $R_b ≈ 5.33 \times 10^5 Ω$ and power dissipated 0.47 W.

 

[ehild]

So $R_b ≈ 5.33 \times 10^5 Ω$ and power dissipated 0.47 W.

It is correct.

ehild