Capacitor circuit, time for current to drop

[scholio]

Homework Statement

the capacitor is originally charged to 100 volts. the switch is closed at t=0. how long does it take for the current to drop to 0.068 amps?

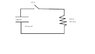
circuit drawing attached

Homework Equations

capacitance C = Q/V where Q is charge, V is electric potential

V = IR where I is current, R is resistance

I = dW/dt where W is work, t is time

I = epsilon/ R_1 + R_2 where epsilon is battery emf, R is resistance

QV/t = I^2R where t is time ---> t = QV/I^2R

The Attempt at a Solution

right now, i am trying to figure out the equation to use, i have a feeling the capacitance formula does not come into play. but there is a capacitance value given in the diagram of 100*10^-6 farads, should i use C = Q/V to find charge Q?

Q = CV = 100*10^-6 (100) = 0.01 coulombs

the variables i do have are R and V, so i can find I using I = V/R = 100/200 = 0.5 ampere

t = QV/I^2R ---> should I be the change in I (0.5 - 0.068 = 0.432)?

t = (0.01*100)/(0.068^2(200)) = 1/0.9248 = 1.08 seconds

did i do it correctly?

 

[rl.bhat]

In RC circuit current increases exponentially. The instantaneous current is gives by
I = Io*e^-t/RC where Io = V/R

 

[scholio]

okay so use that equation i got this:

0.068 = (100/200)e^(-t/(200(100*10^-6)))
0.136 = e^(-t/0.02)
ln(0.136) = -t/0.02
-t = -0.039 = 0.04 seconds

does that make sense?