Jack99123
- 2
- 0
- Homework Statement
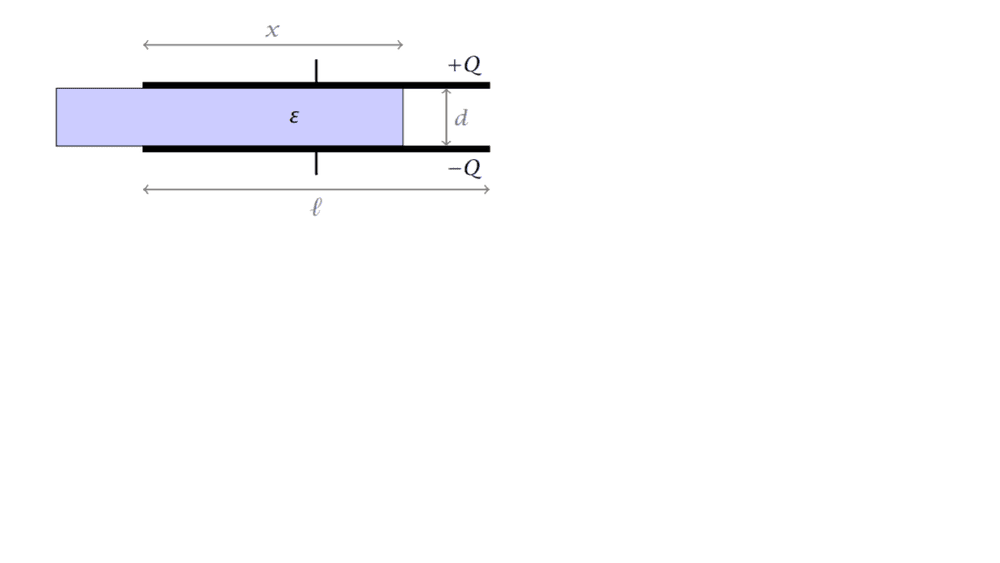
- Between two conducting plates (length ## l ##, width ## w ## and distance ## d ##) there is an insulator (permittivity \epsilon). The capacitor is charged with voltage ## V ## (charge ## Q ##). After this the voltage source is removed. The insulator is moved to the left in the direction of ## l ## a distance ## l-x ##. Calculate the force that the electric field tries to drag the insulator back
to between the conducting plates. (Hint. F=-∇U, expression for potential energy with
capacitance, the capacitor charge is constant, voltage changes)
- Relevant Equations
- ##C_e=C_1+C_2##
##U=\frac{1}{2}*C*V^2##
##C=\epsilon \frac{A}{d} ##
##\vec F =-\nabla U##
First, I think that I need to calculate the capacitance. It is ## C=\epsilon_0*\frac{l*w}{d}-x*\frac{w*\epsilon_0}{d}+\epsilon*\frac{x*w}{d} ##. After that I should calculate the potential energy. It is ##U=\frac{1}{2}*C*V^2 ##. After that I should take its gradient to get the force. So ##\vec F =-\nabla U=-\frac{d}{dx}U*\vec i=-\frac{(\frac{-w*\epsilon_0}{d}+\frac{\epsilon*w}{d})*v^2}{2}*\vec i ##
. Is this correct and if it's not, could you please help me?
. Is this correct and if it's not, could you please help me?
Last edited: