- #1
samieee
- 67
- 0
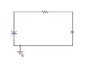
We know charge is accumulated on the conductor plates of capacitor. Here is a circuit (image) with voltage source, resistor and capacitor. Now due to the capacitor the circuit is actually open so flow of charge aka current is zero. Then how can charge be accumulated on the plates of capacitor?