- #1
CAF123
Gold Member
- 2,948
- 88
Homework Statement
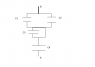
Calculate the capacitance between A and B in the attached diagram.
(Capacitor.png)
The Attempt at a Solution
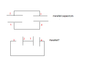
I just want to clarify something in my book first: The definition for capacitors in parallel is given as 'the capacitors are directly wired together at one plate and directly wired together at the other plate..' So something like in the top picture of (Parallel.png). However, with the defintion given, I can also draw the bottom picture of Parallel.png which means (according to that defintion) that system is also in parallel. This does not seem right because there is only passage for charge through the circuit. Is the definition in the book a little vague or did I miss something?
Many thanks.