Cartesian to Cyclindrical Coordinate

[destroyer130]

Problem

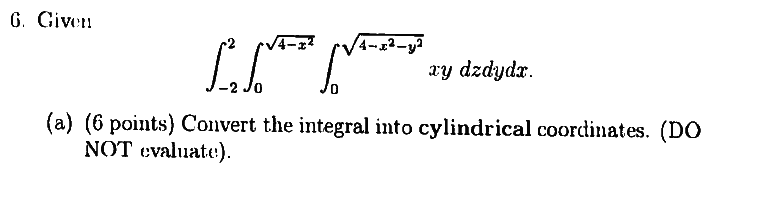
Solution answer

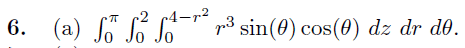
For this one, my upper bound of z in cylindrical's is sqrt(4-r^2) instead of (4-r^2). Which one is right, mine or the solution? Thanks for helping me out.

 

[Dick]

Problem
View attachment 54032
Solution answer
View attachment 54033
For this one, my upper bound of z in cylindrical's is sqrt(4-r^2) instead of (4-r^2). Which one is right, mine or the solution? Thanks for helping me out.

I'd say you are right. Must be a typo.

 

[Bill Nye Tho]

You're right