CoolDude420
- 199
- 9
Homework Statement
Hi,
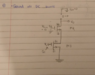
I'm just trying to derive the small-signal model of the cascode MOSFET amplifier circuit. In the lectures, we were just given the small-signal model directly. I'm trying to derive it.
I have almost the exact same thing except where I put the output voltage. In the lectures, it is put between D2 and S1,G2. However when I was deriving it, I put it between Ro2.
My derivation attempt: