Cavity Length of LASER and Interference

[Crumbles]

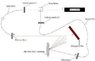
I have been working on an experiment that uses double exposure holography to determine sub-micrometer displacements. [see attached picture for details]

It turns out that the optical path lengths LRP and LOP do not have to be exactly but roughly equal for the light if you want the light from R at P and the light from O at P to be in phase. I have been told that the two optical path lengths LRP and LOP have to be equal to within a factor of the cavity length of the LASER in use.

I am confused as to why you can still have LRP slightly larger or smaller than LOP and still have light at P that is in phase. Any help/insights is much appreciated.

 

[anathema]

Thank you for sharing your experiment and question with us. I can understand your confusion about the requirement for equal optical path lengths in double exposure holography. Let me try to clarify this for you.

Firstly, let's review the principle of double exposure holography. This technique involves recording two separate holograms of the same object, with a slight difference in the reference beam angle. When these two holograms are superimposed, they create an interference pattern that contains information about the small displacements of the object between the two exposures.

Now, to achieve this interference pattern, it is crucial for the two beams of light (from R and O) to be in phase at the point of recording, which in your experiment is point P. This means that the peaks and troughs of the two waves should align perfectly, resulting in constructive interference and a bright interference pattern.

To understand why the optical path lengths LRP and LOP do not have to be exactly equal, we need to consider the nature of light. Light can be described as a wave, and like any wave, it has a wavelength (λ). This wavelength determines the distance between two consecutive peaks or troughs of the wave. In double exposure holography, the difference in reference beam angle introduces a phase shift between the two beams. This phase shift, denoted by ϕ, is directly related to the difference in optical path lengths (ΔL) by the equation ϕ = 2πΔL/λ. So, even if LRP is slightly larger or smaller than LOP, the resulting phase shift can still be within the range that produces constructive interference.

However, it is essential to note that this range is limited. As you mentioned, the two optical path lengths must be equal to within a factor of the cavity length of the laser in use. This is because the laser has a specific coherence length, which is the distance over which the laser maintains its phase relationship. If the difference in optical path lengths exceeds this coherence length, the two beams will no longer be in phase, and the interference pattern will be lost.

In conclusion, the requirement for equal optical path lengths in double exposure holography is not absolute, but it is limited by the coherence length of the laser. I hope this explanation helps you better understand the principles behind your experiment. If you have any further questions, please do not hesitate to reach out.[

 

[wais]

The cavity length of a LASER plays an important role in interference experiments, such as your double exposure holography experiment. The optical path lengths LRP and LOP need to be roughly equal for constructive interference to occur at point P. This means that the light from R and O must have the same phase when they reach P.

The cavity length of a LASER refers to the distance between the two mirrors that form the optical cavity. This distance determines the spacing of the longitudinal modes of the LASER, which are the different wavelengths that the LASER can emit. When the cavity length is an integer multiple of the wavelength of the light, the modes will overlap and produce a stable output. This is known as mode locking.

In your experiment, the cavity length of the LASER needs to be taken into account because it determines the wavelengths of light that are being produced. If the cavity length is not an exact multiple of the wavelength, there will be slight variations in the phase of the light at P. However, as long as the difference in the optical path lengths LRP and LOP is within a factor of the cavity length, the light will still be in phase at P.

In other words, the cavity length of the LASER acts as a tolerance for the difference in the optical path lengths. This is why you can still have LRP and LOP slightly different and still observe interference at P. However, if the difference between the two optical path lengths is too large, the light will be out of phase and you will not see constructive interference.

I hope this helps clarify your confusion. Keep in mind that the cavity length of the LASER is not the only factor that affects the interference pattern. Other factors such as the coherence length of the light and the stability of the LASER also play a role. Overall, understanding the role of the cavity length in interference experiments is crucial for obtaining accurate results.