pinkyboo
- 3
- 0
Centripetal force problems for dynamics :)
I have two questions!
1. You are driving at a speed of 60.0km/h around a turn with a radius of 75m. The coefficient of friction between the tires and the road is 0.85.
a. After traveling 20° around the turn, you hit a patch of ice and your coefficient of friction is reduced to 0.15. After 5 seconds, where are you with respect to the start of the turn?
b. Repeat question a. with a banked curve of 35°.
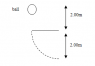
2. A 2.00kg ball is dropped, it sticks to a rope, and makes a circular motion (see below). What is the net force on the banana at the bottom of the swing. (Assume the velocity is constant once it hits the rope... or, for more accuracy, use the conservation of energy formulas)
Fnet = mac
ac = mv2/r
ac = 4∏2r/T2
(first question)
v = 16.6666667m/s, r = 75m, μ = 0.85
For this one, I'm not even really sure where to start. :(
I wanted to do the Fnet = m x 4∏2r/T2 equation, but since I don't have the period, I wasn't really sure where to go at all. Furthermore, part b just boggles me
I also wanted to find FN or just do something concerning the normal or friction forces since I do have the coefficient of friction, but again, without the mass, I'm at a loss.
(second question)
I attached the diagram of the question.
m = 2.00 kg
Grrrr... with this one, I tried to make an FBD, but all attempts were futile! I tried to make Fgx in the direction of the motion, but I'm at a loss for this question as well.
Sorry my attempts at any solutions seem so juvenile, but I really am not sure what to do. Any help would be greatly appreciated!
Homework Statement
I have two questions!
1. You are driving at a speed of 60.0km/h around a turn with a radius of 75m. The coefficient of friction between the tires and the road is 0.85.
a. After traveling 20° around the turn, you hit a patch of ice and your coefficient of friction is reduced to 0.15. After 5 seconds, where are you with respect to the start of the turn?
b. Repeat question a. with a banked curve of 35°.
2. A 2.00kg ball is dropped, it sticks to a rope, and makes a circular motion (see below). What is the net force on the banana at the bottom of the swing. (Assume the velocity is constant once it hits the rope... or, for more accuracy, use the conservation of energy formulas)
Homework Equations
Fnet = mac
ac = mv2/r
ac = 4∏2r/T2
The Attempt at a Solution
(first question)
v = 16.6666667m/s, r = 75m, μ = 0.85
For this one, I'm not even really sure where to start. :(
I wanted to do the Fnet = m x 4∏2r/T2 equation, but since I don't have the period, I wasn't really sure where to go at all. Furthermore, part b just boggles me

I also wanted to find FN or just do something concerning the normal or friction forces since I do have the coefficient of friction, but again, without the mass, I'm at a loss.
(second question)
I attached the diagram of the question.
m = 2.00 kg
Grrrr... with this one, I tried to make an FBD, but all attempts were futile! I tried to make Fgx in the direction of the motion, but I'm at a loss for this question as well.
Sorry my attempts at any solutions seem so juvenile, but I really am not sure what to do. Any help would be greatly appreciated!