bumblebeeliz
- 38
- 0
Centripetal Force / Tension / Speed (HELP!)
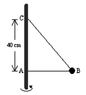
A 100 g bead is free to slide along an 80 cm long piece of string ABC. The ends of the string are attached to a vertical pole at A and C, which are 40 cm apart. When the pole is rotated about its axis, AB becomes horizontal.
a. Find the tension in the string.
b. Find the speed of the bead at B.
Fr= mv2 / r
v= 2\pir / T
v= \sqrt{}m /r ?
Ft = Fn - mg?
m = 100g = 0.1m
length =80cm
radius = 40cm? = 0.4
I drew a free-body diagram with just the beed. Normal force going up, mg going down and tension going towards the pole on line A and C.
I think b) is:
v= \sqrt{} rg
= \sqrt{} 0.4m * 9.80m/s2
= 1.979 m/s
I usually know where to go from here but I am really stuck with the Tension.
Any ideas? :)
Homework Statement
A 100 g bead is free to slide along an 80 cm long piece of string ABC. The ends of the string are attached to a vertical pole at A and C, which are 40 cm apart. When the pole is rotated about its axis, AB becomes horizontal.
a. Find the tension in the string.
b. Find the speed of the bead at B.
Homework Equations
Fr= mv2 / r
v= 2\pir / T
v= \sqrt{}m /r ?
Ft = Fn - mg?
The Attempt at a Solution
m = 100g = 0.1m
length =80cm
radius = 40cm? = 0.4
I drew a free-body diagram with just the beed. Normal force going up, mg going down and tension going towards the pole on line A and C.
I think b) is:
v= \sqrt{} rg
= \sqrt{} 0.4m * 9.80m/s2
= 1.979 m/s
I usually know where to go from here but I am really stuck with the Tension.
Any ideas? :)
Attachments
Last edited: