Challenging Integral Homework: Attempting x=tanA/b Substitution

[Physics lover]

Homework Statement

The question is in Attempt at a solution.

Relevant Equations

x=tanA/b

Homework Statement: The question is in Attempt at a solution.
Homework Equations: x=tanA/b

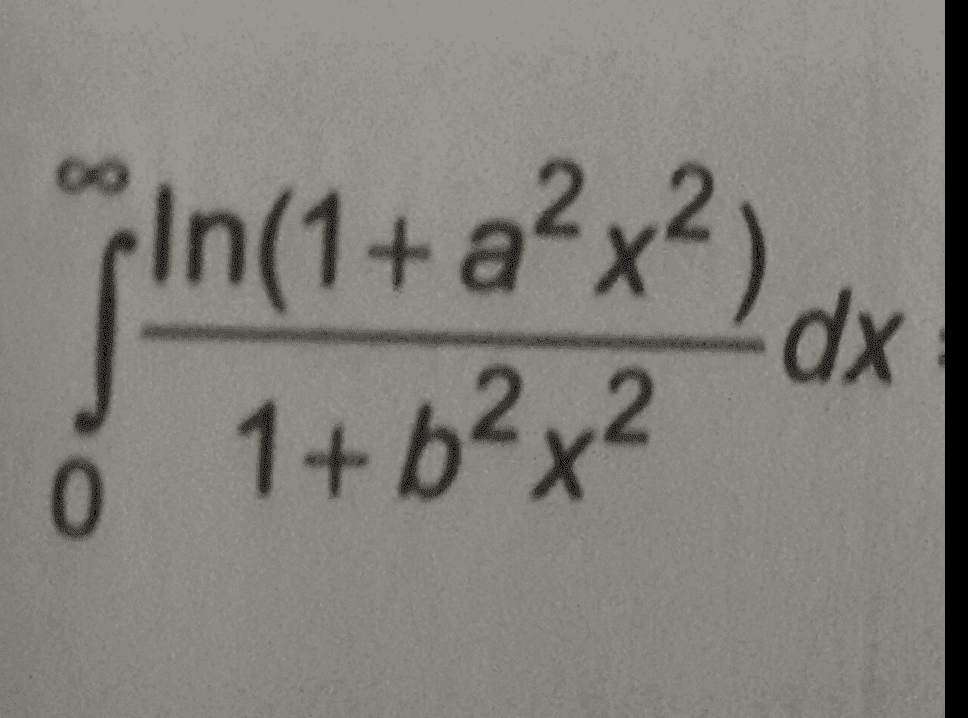
I tried by substituting x=tanA/b but it did'nt helped.Now I cannot think of any other thing to do.Help.

 

[Delta2]

we can write the integrand as $$\frac{\ln(a^2(\frac{1}{a^2}+x^2))}{b^2(\frac{1}{b^2}+x^2)}=\frac{2\ln a}{b^2}\frac{1}{\frac{1}{b^2}+x^2}+\frac{1}{b^2}\frac{\ln(\frac{1}{a^2}+x^2)}{\frac{1}{b^2}+x^2}$$ and now you got to calculate two integrals, the first (left) integral is obvious and straightforward, for the second (right) integral maybe the substitution $y=x^2$ helps.

 

[Physics lover]

we can write the integrand as $$\frac{\ln(a^2(\frac{1}{a^2}+x^2))}{b^2(\frac{1}{b^2}+x^2)}=\frac{2\ln a}{b^2}\frac{1}{\frac{1}{b^2}+x^2}+\frac{1}{b^2}\frac{\ln(\frac{1}{a^2}+x^2)}{\frac{1}{b^2}+x^2}$$ and now you got to calculate two integrals, the first (left) integral is obvious and straightforward, for the second (right) integral maybe the substitution $y=x^2$ helps.

thanks for telling but i cannot simplify the second term.$y=x^2$ didn't helped me a lot.

 

[Delta2]

Yes sorry, originally I thought that it can be simplified to $\frac{\ln(\alpha+y)}{\beta+y}$ and the integral of that doesn't converge but now I see I was wrong.

 

[Physics lover]

Yes sorry, originally I thought that it can be simplified to $\frac{\ln(\alpha+y)}{\beta+y}$ and the integral of that doesn't converge but now I see I was wrong.

Ok no problem.Can you suggest any other method?

 

[Delta2]

Ok no problem.Can you suggest any other method?

No sorry maybe @fresh_42 can enlighten us here. I tried the integral at wolfram and it converges to a hefty expression, but i am not a subscriber there so i can't see the intermediate steps.
https://www.wolframalpha.com/input/?i=integral+(ln(1+a^2x^2))/(1+b^2x^2)+from+0+to++infinite
EDIT:I See the above link doesn't work properly sorry for that.

 

[fresh_42]

WolframAlpha at least indicates that there is no easy closed form. In fact the impression it produces is even hard to differentiate for a cross check. But most important, it looks as if the integral doesn't converge since there is a term $\log(1+a^2x^2)$ which doesn't vanish.

 

[Physics lover]

WolframAlpha at least indicates that there is no easy closed form. In fact the impression it produces is even hard to differentiate for a cross check. But most important, it looks as if the integral doesn't converge since there is a term $\log(1+a^2x^2)$ which doesn't vanish.

But the question is printed in a book and may not be incorrect.So Can you think of any method?

 

[fresh_42]

But the question is printed in a book and may not be incorrect.So Can you think of any method?

The usual tricks are: get rid of what disturbs and look out for symmetries.
So basically we have an integrand $f \cdot f'$ which is the derivative of $f^2$. However, this would be the case if $a=b$, hence this asymmetry is what prevents us from solving it, i.e. we must get rid of the asymmetry first. We can shift it into the translation term: $\log (1+a^2x^2) \sim \log (c^2+x^2)$ and $1+b^2x^2\sim d^2+x^2$. Since the translation part is irrelevant for the $f\cdot f'$ form, this could work. But I haven't tried.

I have only found a formula for $\displaystyle{\int_0^\infty} \dfrac{\log x}{(x+a)(x+b)}dx$.

 

[George Jones]

The original integral probably converges because, for large $x$, $1/\left( 1 + b^2 x^2 \right)$ kills $\ln \left( 1 + b^2 x^2 \right)$.

I tried $a=2$ and $b=3$, and Maple gives a vey simple answer.

Note that since the integrand is even, $\int^\infty_{-\infty} = 2 \int^\infty_0$. Try doing $\int^\infty_{-\infty}$ by closing the contour in the complex plane.

 

[Physics lover]

The original integral probably converges because, for large $x$, $1/\left( 1 + b^2 x^2 \right)$ kills $\ln \left( 1 + b^2 x^2 \right)$.

I tried $a=2$ and $b=3$, and Maple gives a vey simple answer.

Note that since the integrand is even, $\int^\infty_{-\infty} = 2 \int^\infty_0$. Try doing $\int^\infty_{-\infty}$ by closing the contour in the complex plane.

sorry but I didn't understood what you said.Can you be more precise.

 

[Delta2]

sorry but I didn't understood what you said.Can you be more precise.

I think he means to evaluate the integral using contour integrals and complex analysis's methods (Cauchy's integral theorem). Is this exercise from a book for real analysis or complex analysis?

 

[George Jones]

sorry but I didn't understood what you said.Can you be more precise.

I was purposely being imprecise in order to give you something to mull over.

I think he means to evaluate the integral using contour integrals and complex analysis's methods (Cauchy's integral theorem).

Yes, this is what I meant.

Complex contour integration, the residue theorem and often Jordan's Lemma sometimes can be used to evaluate real definite integrals. If you have not seen this stuff, then, as Emily Litella (aka Gilda Radner) says, "Never mind."

Is this exercise from a book for real analysis or complex analysis?

Yes, @Physics lover , some context might help. What are the titles of the book, chapter, and section in which this problem appears?

When I tell Maple (a symbolic math pogramme) that $b>a>0$, Maple gives a horribly complicated answer for the integral. When I include Maple's "simplify" command, Maple spits out
$$\frac{\pi}{b} \left[ \ln\left(a+b\right) - \ln\left(b\right) \right].$$

 

[Delta2]

Wolframalpha gives the result as $$\frac{\pi}{2|b|}(\ln{(1-\frac{a^2}{b^2})}+2\tanh^{-1}(\frac{|a|}{|b|}))$$
which I think simplifies to the same as maple if $b>a>0$ hence $2\tanh^{-1}(\frac{|a|}{|b|})=\ln{\frac{b+a}{b-a}}$

 

[George Jones]

Wolframalpha gives the result as $$\frac{\pi}{2|b|}(\ln{(1-\frac{a^2}{b^2})}+2\tanh^{-1}(\frac{|a|}{|b|}))$$

It is often useful to be able to transform back and forth between inverse hyperbolic trig functions and $\ln$.

For example, if $y = \tanh^{-1}x$, then
$$x = \tanh y = \frac{e^y - e^{-y}}{e^y + e^{-y}}$$

Now, multiply top and bottom by $e^y$, solve for $e^{2y}$, and take the $\ln$ of both sides. I think that this trransforms the WolphramAlpham result into the Maple result.

 

[Physics lover]

I was purposely being imprecise in order to give you something to mull over.
Yes, this is what I meant.

Complex contour integration, the residue theorem and often Jordan's Lemma sometimes can be used to evaluate real definite integrals. If you have not seen this stuff, then, as Emily Litella (aka Gilda Radner) says, "Never mind."
Yes, @Physics lover , some context might help. What are the titles of the book, chapter, and section in which this problem appears?

The problem is from a Aakash Problem Package.From Section-H.

When I tell Maple (a symbolic math pogramme) that $b>a>0$, Maple gives a horribly complicated answer for the integral. When I include Maple's "simplify" command, Maple spits out
$$\frac{\pi}{b} \left[ \ln\left(a+b\right) - \ln\left(b\right) \right].$$
[/QUOTE]Surprisingly,This is the right answer.But did you arrive at that.Please explain.