infk
- 21
- 0
Homework Statement
Homework about a result in probability theory, but I don't understand one of the steps:
Let f(x) be the PDF of a continuous R.V which takes only non-negative values.
Why is the following true?
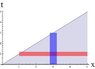
\int^{\infty}_0\int^{\infty}_xf(t) \mathrm{d}t \mathrm{d}x =
\int^{\infty}_0\int^{t}_0f(t)\mathrm{d}x\mathrm{d}t
Homework Equations
N/A
The Attempt at a Solution
We can change the order of integration but I only come up with:
\int^{\infty}_0\int^{\infty}_xf(t)\mathrm {d}t\mathrm {d}x = \int^{\infty}_x\int^{\infty}_of(t)\mathrm {d}x\mathrm {d}t =