Change of flux in an L-R circuit

[arnab321]

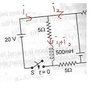
Homework Statement

Homework Equations

afaik, flux in inductor = Li.
at t=0, current through L is 0. so change of flux = LΔi = L(i-0)=Li

The Attempt at a Solution

at t=∞, i through cap. is 0.

so,

i get the following equations:
5(i1+i2)=20
5(i1+i2)+ 5i₂=10

i get i2=-2 and i1 = 6
i through indctor = i1+i2 = 4

so, flux=Li= 0.5*4=2


book's ans. is different.

 

[kushan]

t-o current is zero in the inductor lol

 

[kushan]

but capacitor was charged at t-0

 

[vela]

You did everything right except for assuming the current through the inductor is 0 right before the switch is closed.

 

[arnab321]

You did everything right except for assuming the current through the inductor is 0 right before the switch is closed.

Well, um... Current through inductor is i=i0(1-e^(-t/tau)). Putting t=0 in the equation, I get i=0.

 

[vela]

That equation only applies to a simple LR circuit with the initial condition i(0^-)=0. That's not what you have here.

 

[arnab321]

That equation only applies to a simple LR circuit with the initial condition i(0^-)=0. That's not what you have here.

edit: oh I'm sorry I didn't see the battery there before the switch is closed.

I got the ans. 1.5.

 

[vela]

That's not entirely accurate. At steady state, a capacitor acts like an open circuit, and an inductor, like a short circuit. I wouldn't say, however, the opposite is true at the beginning of a transient.

So suppose the switch has been open a long time before t=0. You replace the inductor with a short. What's the current flowing through the upper-left resistor? That will be the initial current through the inductor.