You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Change of variable (involving partial diff.)
Physics news on Phys.org
Sourabh N
- 634
- 0
In your solution for part 3, you have a factor of r3 in the denominator outside the integral (in each of the three integrals). Remember r = x + y + z, so you cannot take it outside the integral.
Your approach for part c looks confusing. We'll talk about part c, let's get through part b first.
Your approach for part c looks confusing. We'll talk about part c, let's get through part b first.
athrun200
- 275
- 0
Sourabh N said:In your solution for part 3, you have a factor of r3 in the denominator outside the integral (in each of the three integrals). Remember r = x + y + z, so you cannot take it outside the integral.
Your approach for part c looks confusing. We'll talk about part c, let's get through part b first.
It seems r=\sqrt{x^{2}+y^{2}+z^{2}}, isn't it?
Sourabh N
- 634
- 0
Ah, ofcourse! My bad.
athrun200
- 275
- 0
Well if I intergrate r at the same time, it becomes \int\frac{x}{({x^{2}+y^{2}+z^{2}})^\frac{3}{2}}
Which is difficult to integrate...
Which is difficult to integrate...
Sourabh N
- 634
- 0
Not really. For example, for x integral take x2 + y2 + z2 = t, then 2xdx = dt and your integral is simply dt/2*(t^1.5)athrun200 said:Well if I intergrate r at the same time, it becomes \int\frac{x}{({x^{2}+y^{2}+z^{2}})^\frac{3}{2}}
Which is difficult to integrate...
athrun200
- 275
- 0
Sourabh N said:Not really. For example, for x integral take x2 + y2 + z2 = t, then 2xdx = dt and your integral is simply dt/2*(t^1.5)
Oh. I forget that I can use substitution.
But how about the new interval?
From 0 to x^2+y^2+z^2?
Sourabh N
- 634
- 0
Common convention is to express potential relative to potential at infinity, so limits would be\infty to x2 + y2 + z2.athrun200 said:Oh. I forget that I can use substitution.
But how about the new interval?
From 0 to x^2+y^2+z^2?
Sourabh N
- 634
- 0
athrun200 said:Now, I find that the integral for x, y and z are the same.
Is that correct now?
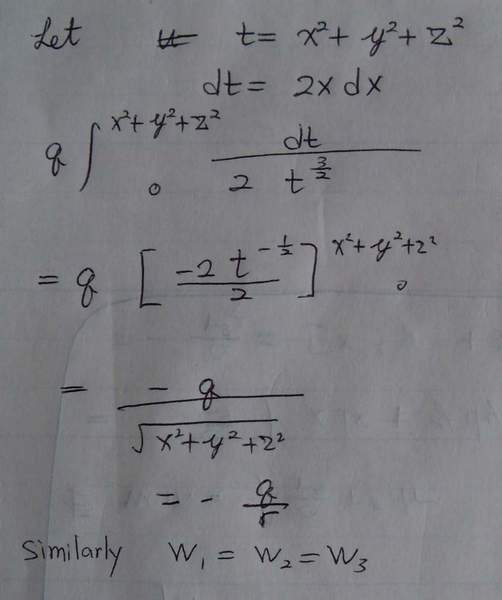
2 things. First, although you wrote 0 as lower limit, you realize it's actually infinity (as I mentioned in previous post). Having the correct upper and lower limit will help you fix the sign of final value for x integral you get.
Second, note it's the x integral; it is accompanied with a \hat{x} and similarly y and z integral are accompanied with respective unit vectors. Together they form \vec{E} which has to look same as 8.11 (this is part c!)
athrun200
- 275
- 0
Do you mean I should put infinty as the upper limit and x^+y^+z^2 as lower limit?Sourabh N said:2 things. First, although you wrote 0 as lower limit, you realize it's actually infinity (as I mentioned in previous post). Having the correct upper and lower limit will help you fix the sign of final value for x integral you get.
What is the physical meaning if I put infinty as the lower limit and x^+y^+z^2 as the upper limit?
Sourabh N said:Second, note it's the x integral; it is accompanied with a \hat{x} and similarly y and z integral are accompanied with respective unit vectors. Together they form \vec{E} which has to look same as 8.11 (this is part c!)
I don't understand this point.
Do you mean that I miss out the vector?
However, inside the integral is a dot product. i.e.F\bullet dr
Since dot product produce scalar only, there should be not any vector left.
Sourabh N
- 634
- 0
Look at it this way - x2 + y2 + z2 = t (where y and z and not constant anymore). So, 2xdx + 2ydy + 2zdz = dt. This substitution makes more sense than taking x2 + y2 + z2 = t with y and z constant as I had suggested previously. Because now the limit of integral is infinity and x2 + y2 + z2. I am not sure about limits of the integral if y and z are kept constant.athrun200 said:Do you mean I should put infinty as the upper limit and x^+y^+z^2 as lower limit?
What is the physical meaning if I put infinty as the lower limit and x^+y^+z^2 as the upper limit?
On the meaning of upper lower limits - Griffith defines potential like
I don't understand this point.
Do you mean that I miss out the vector?
However, inside the integral is a dot product. i.e.F\bullet dr
Since dot product produce scalar only, there should be not any vector left.
Ignore this. I jumped on part c in my head.
Last edited:
athrun200
- 275
- 0
Sourabh N said:Look at it this way - x2 + y2 + z2 = t (where y and z and not constant anymore). So, 2xdx + 2ydy + 2zdz = dt. This substitution makes more sense than taking x2 + y2 + z2 = t with y and z constant as I had suggested previously. Because now the limit of integral is infinity and x2 + y2 + z2. I am not sure about limits of the integral if y and z are kept constant.
On the meaning of upper lower limits - Griffith defines potential like View attachment 37100 I cannot possibly give a better explanation. I highly recommend you have a look (Sec 2.3 in Griffith - Intro to electrodynamics)
Ignore this. I jumped on part c in my head.
So \phi=\frac{q}{r}?
If it is correct, let's move to part c.
I would like to know if I get the correct cylindrical form.
Sourabh N
- 634
- 0
Yes that is correct. You can check that by using \vec{E} = -\nabla \phi and comparing it with 8.11athrun200 said:So \phi=\frac{q}{r}?
If it is correct, let's move to part c.
To get \phi in cylindrical form, you have to write \vec{E} in cylindrical coordinates and follow the procedure as above. (To know how to go to cylindrical from spherical, look at http://is.gd/JFitBh)I would like to know if I get the correct cylindrical form.
athrun200
- 275
- 0
Sourabh N said:To get \phi in cylindrical form, you have to write \vec{E} in cylindrical coordinates and follow the procedure as above. (To know how to go to cylindrical from spherical, look at http://is.gd/JFitBh)
Do you mean that my approach above can't get the answer?
If so, why?
Similar threads
- Replies
- 5
- Views
- 4K
- Replies
- 1
- Views
- 2K
- Replies
- 5
- Views
- 1K
- Replies
- 1
- Views
- 1K
- Replies
- 5
- Views
- 1K
- Replies
- 6
- Views
- 2K
- Replies
- 6
- Views
- 1K
- Replies
- 9
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 3
- Views
- 3K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 105
- Calculus and Beyond Homework Help
-
Solve this problem that involves induction
- Started by chwala
- Replies: 7
- Calculus and Beyond Homework Help
-
Finding the modulus and argument of ##\dfrac{a}{(b±ci)^n}##
- Started by chwala
- Replies: 17
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math