Changing format of the equation of interpolation

[Bruno Tolentino]

Give 2 points: (a, f(a)) and (b, f(b)), is possible plot a line function L(x) that intersects these two points, the linear function is:

$$L(x) = f(b) \frac{(x - a)}{(b-a)} + f(a) \frac{(x-b)}{(a-b)}$$

In other format, is:

$$L(x)-f(a) = \frac{f(b)-f(a)}{(b-a)} (x-a)$$

Now, given 3 points: (a, f(a)), (m, f(m)) and (b, f(b)), is possible too plot a quadratic function P(x) that intersects these three points, and the quadratic function is:

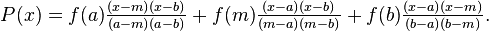
And what I REALLY WANT is change the format of the function P(x) for a new format of equation where all factors are the form (u-v).

Here are some relationships that can help you to help me:
https://en.wikipedia.org/wiki/Linear_equation#Two-point_form
https://en.wikipedia.org/wiki/Linear_equation#2D_vector_determinant_form
https://en.wikipedia.org/wiki/Simpson's_rule#Quadratic_interpolation
https://pt.wikipedia.org/wiki/Polinômio_de_Lagrange#Polin.C3.B4mios_de_Lagrange
https://en.wikipedia.org/wiki/Mean_value_theorem
https://pt.wikipedia.org/wiki/Matriz_de_Vandermonde

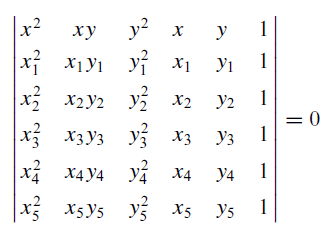
Equation of hyperbola:
$$\left( \frac{x}{a} \right)^2 - \left( \frac{y}{b} \right)^2 = 1$$
Equation of elipse:
$$\left( \frac{x}{a} \right)^2 + \left( \frac{y}{b} \right)^2 = 1$$
Equation of parabola:
$$\left( \frac{x}{a} \right)^2 + \left( \frac{y}{b} \right) = 1$$
Equation of straight line:
$$\left( \frac{x}{a} \right) - \left( \frac{y}{b} \right) = 1$$

This is a horrible question, because involves so much algebraic operations, for this reason I posted all these relationship above, because, maybe you can to get the answer for my question without make counts, just comparing the symmetry...

 

[mathman]

It is not clear in what way what you want is different from the display.

 

[Bruno Tolentino]

Realize that the 2nd equation is of the form: (u-v) = (u-v)/(u-v) * (u-v), all factors are of the form (u-v). This is not true for the 1nd equation, that is of the form w = w (u-v)/(u-v) + w (u-v)/(u-v), the same happens with the 3nd equation, I would like of rewrite all factors in the form (u-v), obviously, P(x), f(a), f(m) and f(b) are separated factors.

 

[Bruno Tolentino]

EDIT: I got my answer!

Calling a of x₃, m of x₂ and b of x₁ and f(a) of y₃, f(m) of y₂ and f(b) of y₃, the answer for my question is:

$$(y - y_1) = \frac{(y_3 - y_1)}{(x_3 - x_2)(x_3 - x_1)} (x-x_2)(x-x_1) + \frac{(y_2 - y_1)}{(x_2 - x_1)(x_2 - x_3)} (x-x_1)(x-x_3)$$

BUT, my second question is: is possible isolate all the y terms in the left side of equation and isolate all the x terms in the right side? (independent of the format of equation, the important, for my is just isolate the terms x and y) If yes, so, you can help me make this?