Charged particles arranged in tetrahedron

[utkarshakash]

Homework Statement

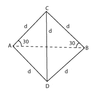
Four charged particles (A, B, C, D), of mass m and charge q each, are connected by light silk threads of length d forming a tetrahedron floating in outer space. The thread connecting particles A and B suddenly snaps. Find the maximum speed of particle A after that.

The Attempt at a Solution

I'm trying to use conservation of energy. The initial potential energy of the system will be
\dfrac{6q^2}{4 \pi \epsilon_0 d}

But I can't realize when will the speed of particle A be maximum. Also, what will be the speed of other particles at that instant? Will they be equal.

 

[projjal]

. The initial potential energy of the system will be
\dfrac{4q^2}{4 \pi \epsilon_0 d}

I think that's not correct.

 

[utkarshakash]

I think that's not correct.

Sorry. My bad. Replace 4 with 6.

 

[dauto]

The maximum speed (and maximum kinetic energy) is achieved when the particle A and B swing the furthermost from each other (minimizing potential energy).

 

[utkarshakash]

The maximum speed (and maximum kinetic energy) is achieved when the particle A and B swing the furthermost from each other (minimizing potential energy).

Would the final arrangement of particles be like this (see attached image) ?

 

[Saitama]

Would the final arrangement of particles be like this (see attached image) ?

Looks right to me, so what is the final potential energy? (Notice that you look for change in potential energy, you don't have to write down the complete expression for final potential energy)

 

[dauto]

Would the final arrangement of particles be like this (see attached image) ?

Yes, except that the triangles ought to be equilateral.

 

[utkarshakash]

Yes, except that the triangles ought to be equilateral.

This means one of the strings wouldn't be taut then, right?

 

[SammyS]

This means one of the strings wouldn't be taut then, right?

Yes, the one which snapped .

 

[utkarshakash]

Yes, the one which snapped .

No. I'm talking about the strings except the one which snapped. According to dauto the triangles won't be equilateral. What, then, will be the length of sides of the triangle so formed?

 

[TSny]

According to dauto the triangles won't be equilateral.

In post #7 dauto said the triangles will be equilateral.

 

[ehild]

No. I'm talking about the strings except the one which snapped. According to dauto the triangles won't be equilateral. What, then, will be the length of sides of the triangle so formed?

No dauto said that the triangles should be equilateral. They did not look like that in your picture.

ehild

 

[utkarshakash]

No dauto said that the triangles should be equilateral. They did not look like that in your picture.

ehild

Looks like I misunderstood his post.

I got the correct answer.

 

[TSny]

I got the correct answer.

Nice. Good work!

 

[dauto]

May be I ought not use the word ought...

 

[TSny]

May be I ought not use the word ought...

------------

By the way, utkarshakash. Did you find that all 4 of the particles have the same speed when particle A has maximum speed?

 

[utkarshakash]

------------

By the way, utkarshakash. Did you find that all 4 of the particles have the same speed when particle A has maximum speed?

Yes. But I still have doubt why they would all have the same speed.

 

[TSny]

Yes. But I still have doubt why they would all have the same speed.

Can you describe the motion of the center of mass of the system after the string is cut?

 

[utkarshakash]

Can you describe the motion of the center of mass of the system after the string is cut?

Initially the center of mass is at rest. The net external force on the system is zero as tension forces are internal to it. Thus, the COM will remain at rest even after the string is cut and so, the particles will have same speed in opposite directions. Is this explanation correct?

 

[TSny]

Yes, the COM must remain at rest. The 4 particles will not have the same speed at arbitrary times, but you should be able to argue that they have the same speed at the instant of time when all 4 particles lie in the same plane.

 

[Vibhor]

Yes, the COM must remain at rest. The 4 particles will not have the same speed at arbitrary times, but you should be able to argue that they have the same speed at the instant of time when all 4 particles lie in the same plane.

Isn't it possible that A and B move with same speed and C and D move with same speed(but different from A and B) ? The COM in this case remains at rest .

 

[dauto]

Isn't it possible that A and B move with same speed and C and D move with same speed(but different from A and B) ? The COM in this case remains at rest .

Yes, but when the maximum extension of the swing is reached and the particle configuration is planar The speeds of A and B must be equal and opposite to the speeds of C and D because all the speeds will be collinear and perpendicular to the plane containing the particles.

 

[haruspex]

This means one of the strings wouldn't be taut then, right?

According to my calculations, string CD will go slack. That makes the problem a whole lot more complicated. If I'm right, the book answer is wrong.

 

[TSny]

According to my calculations, string CD will go slack. That makes the problem a whole lot more complicated. If I'm right, the book answer is wrong.

That's interesting. I didn't even think to check if CD would go slack!

Right now, when I do the calculations I'm getting that CD doesn't go slack. But my attempt at the calculation is messy and tedious. Every time I recheck it, I find mistakes. Just a factor of 2 somewhere can make all the difference. So, I'm not confident. But at this point I'm getting tension in CD all the way through the motion.

 

[haruspex]

That's interesting. I didn't even think to check if CD would go slack!

Right now, when I do the calculations I'm getting that CD doesn't go slack. But my attempt at the calculation is messy and tedious. Every time I recheck it, I find mistakes. Just a factor of 2 somewhere can make all the difference. So, I'm not confident. But at this point I'm getting tension in CD all the way through the motion.

OK, here are my calcs.
Let $K=\dfrac{q^2}{4 \pi \epsilon_0 d^2}$.
Initial PE = 6Kd. Assume CD stays taut. When planar, PE = 5Kd+Kd/√3, so PE loss = Kd(1-1/√3).
If each particle now has speed v, KE = 2mv².
Here's a tricky bit: the instantaneous axis of rotation of the triangle ACD is the line joining the midpoints of AC, AD. So the radius of rotation of A is d(√3)/4. the centripetal force = $\frac{mv^2}{d\frac{\sqrt 3}{4}} = 2K\frac{\sqrt 3 - 1}{3}$
Let the tension in AC be T. The electrostatic repulsion A feels from B, C and D in the BA direction is K(√3+1/√3).
Hence T√3 = K(√3+1/√3)+mv²/(d(√3)/4) = $K\left(\sqrt 3+\frac {1}{\sqrt 3}+\frac{2\sqrt 3 - 2}{3}\right) = 2K(\sqrt 3 - \frac 13)$
The tensions in CA, CB etc. also act to pull C and D together. The force that way on C due to strings AC and BC = T = 2K(1-1/√3).
The electrostatic force acting oppositely on C is K(1+1/2+1/2) = 2K. There is no centripetal force required of CD.
√3 - 1/3 > 1, yes?

Edit: I think I've underestimated the centripetal acceleration of A by a factor of 2. The triangle ACD as a whole is accelerating towards the line where CD is at that instant. This will serve to make CD go slack even more surely.

 

[TSny]

Here's a tricky bit: the instantaneous axis of rotation of the triangle ACD is the line joining the midpoints of AC, AD. So the radius of rotation of A is d(√3)/4.

As you noted in your edit, the radius of rotation is half this amount: d(√3)/8.

Particle A moves on an ellipse with semi-major axis a = d(√3)/2 and semi-minor axis b = d(√3)/4. The radius of curvature of the ellipse at the point of interest is b²/a = d(√3)/8.

Let the tension in AC be T. The electrostatic repulsion A feels from B, C and D in the BA direction is K(√3+1/√3).

I get that the net electrostatic repulsion on A is K(√3+1/3)

I then get that √3T_AC = K(7/√3 -1), or T_AC = K(7/3-1/√3).

I agree with the rest of your calculation, but I'm finding that making the correction for T_AC yields a tension T_CD = K(√3 -1)/3.

 

[haruspex]

As you noted in your edit, the radius of rotation is half this amount: d(√3)/8.

Particle A moves on an ellipse with semi-major axis a = d(√3)/2 and semi-minor axis b = d(√3)/4. The radius of curvature of the ellipse at the point of interest is b²/a = d(√3)/8.



I get that the net electrostatic repulsion on A is K(√3+1/3)

I then get that √3T_AC = K(7/√3 -1), or T_AC = K(7/3-1/√3).

I agree with the rest of your calculation, but I'm finding that making the correction for T_AC yields a tension T_CD = K(√3 -1)/3.

I agree with all that. But my key error was right near the end, where I used the formula for T√3 instead of that for T .

Thanks!

 

[dauto]

Now the question is if q_A = q_B, and q_C = q_D, but q_C = σq_A, what must σ be in order for the central string to go slack.