Charges of two capacitors in a circuit

[boomerang22]

Homework Statement

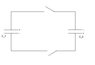
Capacitors C_1=6μF and C_2=2μF are first charged by connecting them in parallel across a 250V battery. The capacitors are then disconnected from the battery and connected positive plate to negative plate and negative plate to positive plate. Calculate their charges after the switches are closed (figure attached).

The answer is given: Q_1=750μC and Q_2=250μC.

Homework Equations

Q=CV Where Q is the charge, C is the capacitance and V is the voltage.

The Attempt at a Solution

I'm really at a loss in how to approach this problem. I'm not even sure whether the capacitors are considered to be in series or in parallel. Since the positive plates are connected to the negative ones I assumed it was in series but in series the charges on capacitors are the same which can't be right since for the final answer the charges between the two are different. I then tried it if the capacitors were in parallel, but that would mean the voltages of both capacitors must be the same as well, meaning that the final charges should equal the original charges on the capacitors since they were both charged to a voltage of 250V, which is also wrong.

 

[Woopy]

''The capacitors are then disconnected from the battery and connected positive plate to negative plate and negative plate to positive plate.''

This part means they are parallel. Try drawing it out and you will see if you make the plates connect as described.

 

[boomerang22]

Hmm... I tried to attach the figure on the first post but I guess it didn't work. The thing is though, even if they are in parallel, their initial voltages are the same, and when capacitors are connected in series their voltages are supposed to be the same. So if both capacitors already have a voltage of 250V before they are connected then shouldn't it stay the same after they are connected?

 

[Woopy]

If C1 has 3 times as much ability to store charge, it makes sense it has 3 times as much charge to me

 

[gneill]

Hmm... I tried to attach the figure on the first post but I guess it didn't work. The thing is though, even if they are in parallel, their initial voltages are the same, and when capacitors are connected in series their voltages are supposed to be the same. So if both capacitors already have a voltage of 250V before they are connected then shouldn't it stay the same after they are connected?

Capacitors in series have the same charge IF they start off with the same charge (usually it's zero charge on both). If they have existing charges when they are connected in series, then the discrepancy in charge between the two will be maintained since being in series they must share the same current (and the change in charge for both is I = dQ/dt).

When only two components are involved and they are connected as described then they can be considered to be both in series AND in parallel. The connections satisfy both definitions.

You can take advantage of this to state that they will end up sharing the same voltage, and that any current that flows must flow through both. If you draw a diagram showing the plates of the two capacitors with the charges on each just before they are connected, you might be able to see how the charges, upon "seeing" each other, will move. Expect some mutual cancellation

 

[boomerang22]

Okay, so I put it to numbers and got the answer, I just want to make sure that what I'm saying is makes sense. First I calculated the initial charges on both capacitors using the relationship between charge, capacitance and voltage. So: Q_1=250V*6μF=1500μC and Q_2=250V*2μF=500μC. After they are connected the 500μC stored in capacitor 1 wants to move to the negatively charged plate of capacitor 2 and only 500μC from capacitor 2 wants to move to the negatively charged plate of capacitor 1. So this 500μC becomes part of the current and only 1000μC remain for the capacitors to be charged by. Since Q_1=V*6μF and Q_2=V*2μF and the fact that they have the same voltage in the end, dividing both equations give Q_1/Q_2=3. Then I used that relationship and the fact that Q total equals 1000μC to find the answer. Does that make sense?

 

[gneill]

Okay, so I put it to numbers and got the answer, I just want to make sure that what I'm saying is makes sense. First I calculated the initial charges on both capacitors using the relationship between charge, capacitance and voltage. So: Q_1=250V*6μF=1500μC and Q_2=250V*2μF=500μC. After they are connected the 500μC stored in capacitor 1 wants to move to the negatively charged plate of capacitor 2 and only 500μC from capacitor 2 wants to move to the negatively charged plate of capacitor 1. So this 500μC becomes part of the current and only 1000μC remain for the capacitors to be charged by. Since Q_1=V*6μF and Q_2=V*2μF and the fact that they have the same voltage in the end, dividing both equations give Q_1/Q_2=3. Then I used that relationship and the fact that Q total equals 1000μC to find the answer. Does that make sense?

Yup. That'll do