Circle to cylindrical coordinates

[sci-doo]

Homework Statement

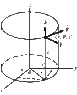
Transform to cylindrical coordinates:
x$$^{2}$$+y$$^{2}$$=R$$^{2}$$

Doesn't look like a problem at all first...

Homework Equations

.. after all I know that is a circle (2d) and we can forget the z-axis (=0) and transform it to just polar coords.
Also I know, that for polar coordinates
x = r cos$$\theta$$
y = r sin$$\theta$$

The Attempt at a Solution

But I don't know how to put it out as an answer. Am I supposed to give a parametric equation in terms of x=... and y=... or should it be like r=... and $$\theta$$=... and z=0 or can I express it without parametres?

 

[sci-doo]

hey, do I get the correct equation just by replacing x with r cos$$\theta$$ and y with r sin$$\theta$$? So that cartesian eq
x$$^{2}$$+y$$^{2}$$=R$$^{2}$$
is
(r cos$$\theta$$)$$^{2}$$+(r sin$$\theta$$)$$^{2}$$=R$$^{2}$$
in cylindrical?

Or should it be something else, like parametric form of some kind?

 

[sci-doo]

(r cos$$\theta$$)$$^{2}$$+(r sin$$\theta$$)$$^{2}$$=R$$^{2}$$
and it all goes down to r=R?

I guess it goes the same way with the spherical coordinates.

I'm sorry for this monoloque.

I hope someone would correct me if I'm wrong. thank you.

 

[HallsofIvy]

Yes, $x^2+ y^2= R^2$ is a cylinder (not a circle) of radius R so it is particulary simple in cylindrical coordinates.

No, it does not "go that way" with spherical coordinates. In spherical coordinates $x= \rho cos(\theta) sin(\phi)$ and $\phi= \rho sin(\theta) sin(\phi)$ so $x^2+ y^2= \rho^2 cos^2(\theta)sin^2(\phi)+ \rho^2 sin^2(\theta)sin^2(\phi)$$= <br /> \rho^2 sin^2(\phi)= R^2$.

 

[sci-doo]

Yes, $x^2+ y^2= R^2$ is a cylinder (not a circle) of radius R so it is particulary simple in cylindrical coordinates.

I think (and still do) that it is a circle, because it has no z.

No, it does not "go that way" with spherical coordinates. In spherical coordinates $x= \rho cos(\theta) sin(\phi)$ and $\phi= \rho sin(\theta) sin(\phi)$ so $x^2+ y^2= \rho^2 cos^2(\theta)sin^2(\phi)+ rho^2 sin^2(\theta)sin^2(\phi)$$= <br /> \rho^2 sin^2(\phi)= R^2$.

Isn't the equation for circle R=r in both cylindrical and spherical coordinates?

 

[sutupidmath]

I think (and still do) that it is a circle, because it has no z.



Isn't the equation for circle R=r in both cylindrical and spherical coordinates?

It is a cylinder, as a matter of fact. Because, it is saying that for any z at all, we have x^2+y^2=R^2.

 

[sci-doo]

It is a cylinder, as a matter of fact. Because, it is saying that for any z at all, we have x^2+y^2=R^2.

If the z is zero, aren't we only left with a circle?

man.. understanding one thing requires not understanding two..

I hope I know how to turn cartesian equations to cylindrical and spherical now.

I'm really trusting on these tricks:

For cylindrical: x^2+y^2=r^2
For spherical: x^2+y^2+z^2=$$\rho$$^2

So if I must for example turn this cartesian
x^2+y^2-z=0
into a speherical equation, i just add both sides z^2 and
x^2+y^2+z^2=z+z^2
$$\rho$$^2=z+z^2
$$\rho$$=$$\sqrt{z+z^2}$$ and because z= $$\rho$$ cos $$\phi$$
$$\rho$$=$$\sqrt{\rho cos \phi +(\rho cos \phi)^2}$$

Most likely I'm wrong. Once again, help is really appreciated.

 

[sutupidmath]

If the z is zero, aren't we only left with a circle?

man.. understanding one thing requires not understanding two..

I hope I know how to turn cartesian equations to cylindrical and spherical now.

I'm really trusting on these tricks:

For cylindrical: x^2+y^2=r^2
For spherical: x^2+y^2+z^2=$$\rho$$^2

So if I must for example turn this cartesian
x^2+y^2-z=0
into a speherical equation, i just add both sides z^2 and
x^2+y^2+z^2=z+z^2
$$\rho$$^2=z+z^2
$$\rho$$=$$\sqrt{z+z^2}$$ and because z= $$\rho$$ cos $$\phi$$
$$\rho$$=$$\sqrt{\rho cos \phi +(\rho cos \phi)^2}$$

Most likely I'm wrong. Once again, help is really appreciated.

That is one way of doing it. You could have also just substitute the values of x,y and z in terms of ro, cos, sin and corresponding angles, and you would have ended up with the same thing.

Note: the reason you can take the square root of $$\rho^2$$ is because it cannot be negative. Otherwise, you would have stepped on the red line...

 

[sutupidmath]

If the z is zero, aren't we only left with a circle?

Well, as a matter of fact, the levle curves of this surface projected in any plane z=k, where k is a constant, are circles.

 

[HallsofIvy]

If the z is zero, aren't we only left with a circle?

Yes, but you are NOT told that z= 0. Because "it has no z", there is no restriction on z: z can be any number.

man.. understanding one thing requires not understanding two.. [\quote]
No, understanding one thing requires understanding two!

I hope I know how to turn cartesian equations to cylindrical and spherical now.

I'm really trusting on these tricks:

For cylindrical: x^2+y^2=r^2
For spherical: x^2+y^2+z^2=$$\rho$$^2

So if I must for example turn this cartesian
x^2+y^2-z=0
into a speherical equation, i just add both sides z^2 and
x^2+y^2+z^2=z+z^2
$$\rho$$^2=z+z^2
$$\rho$$=$$\sqrt{z+z^2}$$ and because z= $$\rho$$ cos $$\phi$$
$$\rho$$=$$\sqrt{\rho cos \phi +(\rho cos \phi)^2}$$

It would be better to leave it as
$$\rho^2$$=$$\rho cos \phi +(\rho cos \phi)^2$$

Most likely I'm wrong. Once again, help is really appreciated.