Geometry Homework: Sum of Circles and Triangles in Figure

[darkmagic]

Homework Statement

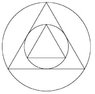
Please see the attached figure
The radius of the biggest circle is 10.
The required is the sum of all circles and the sum of all triangles in the figure.
There is an infinite number of circles and triangles.

My answers are:
for circle: 475/3 pi
for triangle: 175/2 sqrt(3)

I have my solutions please check if they are correct.

 

[HallsofIvy]

That's not what I get.

Each side of triangle cuts the circle in a 360/3 = 120 degree arc.

Taking "r" as a radius of the circle, the two radii and one side of a triangle form a small triangle with 2 sides of length r and angle 120 degrees. By the cosine law, the side of the triangle has length s given by $s^2= r^2+ r^2- 2r*r cos(120)= 2r^2+ 2r^2(-1/2)= 3r^2$ so that $s= r\sqrt{3}$. Dropping a perpendicular from the center of the circle to the side of the triangle gives a right triangle with hypotenuse of length r and one leg of length $(\sqrt{3}/2 )r$. By the Pythagorean theorem, The other leg has length given by $x^2= r^2- (3/4)r^2= (1/4)r^2$ so that $x= r/2$. That is, each circle has radius exactly half the radius of the next larger circle.

If the outermost circle has radius R, then sum of the areas is the geometric series
$$\R^2+ \frac{1}{4}\pi R^2+ \frac{1}{8}\pi R^2+ \cdot\cdot\cdot$$
$$= \pi R^2(1+ \frac{1}{4}+ \frac{1}{8}+ \cdot\cdot\cdot)$$.

 

[darkmagic]

In my solution, first circle is 10 then the second is 5. after that, I used s = a/(1-r). a=25 since 5 will be squared and r=1/4. So my solution is A = pi[10^2 + 5^2 +25/(1-1/4). so my answer becomes 475/3 pi.