hadoque
- 39
- 1
Homework Statement
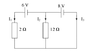
Find the three currents in the image.
Homework Equations
Khirkoffs laws
Sum of currents equal zero.
The potentials around a closed loop add up to zero.
The equations given in the solution are
-2I_1 + 12I_2+6=0
-12I_2+8 = 0
I_1+I_2+I_3=0
The Attempt at a Solution
When I tried to solve this I had the first equation to be
-2I_1-12I_2+6=0, by doing a potential walk round the left subcircuit (?).
Why should the second term be positive?