Circuit question: Why are these R in series and not in parallel?

[Parad0x88]

Homework Statement

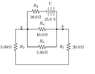
Ok so I don't actually need help to solve the problem and find the currents and voltages for each resistors, that is done and quite easy for me. What I don't understand for this specific problem is why everything in the solution is inverse. For example:

R1 and R2, my reflex would be to say they are in parallel, but in this problem they are in series
R3, R4 and R5, my reflex would be to say they are in parallel, but in this problem, R4 and R5 and in parallel with the new combo R12, and finally R3 is in series with the combo R1234

I am assuming it is due to the fact of where A and B is positioned in the drawing, but I cannot explain it. Any help would be greatly appreciated!

 

[grzz]

Resistors are in series if the current which passes through one also passes through each of the others.

Resistors are in parallel if the potential difference which is across one of them is also the same potential difference which is across each of the others.

 

[1MileCrash]

The key is to take it in steps and pay attention to what the current has to do, it doesn't matter what it looks like. If the current has to pass through one before it can get to the other, it's in series.

Step 1: You can immediately conclude that r4 and r5 are in parallel because current is not forced to go through one before it can get to the other. Make this an equivalent resistance R45p.

Step 2: Once you have done this, it is clear that r1 and r2 must be in series because current must pass through one in order to get to the other. Make this resistance R12s.

Step 3: You now can combine these two equivalent resistances. It is clear they are in parallel because current can flow through R12s or R34p without passing through the other. (If it is hard to visualize, draw each step. I just erase part of the circuit and redraw the eq resistance.)

Step 4: Finally, you are down to two resistors, R3 and ((R12s)(R34p))p. These are clearly in series because current must pass through one to get to the other.

The final singular equivalent resistances is then:

(((R12s)(R34p))p)R3)s

I'm not sure that notation is very clear, I hope this helps.

 

[Parad0x88]

The key is to take it in steps and pay attention to what the current has to do, it doesn't matter what it looks like. If the current has to pass through one before it can get to the other, it's in series.

Step 1: You can immediately conclude that r4 and r5 are in parallel because current is not forced to go through one before it can get to the other. Make this an equivalent resistance R45p.

Step 2: Once you have done this, it is clear that r1 and r2 must be in series because current must pass through one in order to get to the other. Make this resistance R12s.

Step 3: You now can combine these two equivalent resistances. It is clear they are in parallel because current can flow through R12s or R34p without passing through the other. (If it is hard to visualize, draw each step. I just erase part of the circuit and redraw the eq resistance.)

Step 4: Finally, you are down to two resistors, R3 and ((R12s)(R34p))p. These are clearly in series because current must pass through one to get to the other.

The final singular equivalent resistances is then:

(((R12s)(R34p))p)R3)s

I'm not sure that notation is very clear, I hope this helps.

Awesome, thanks! I hadn't learned it this way, but it makes perfect sense!