Circuit that converts a triangular wave potential waveform

[mohlam12]

I have to propose a circuit that converts a triangular wave potential waveform to a square wave potential waveform, that has a T=10ms and Umax= +4V (the triangular curve has the same T and Umax)
We have a capacitor of 4micro Farad and 3 resistance (1kΩ ; 250Ω ; 500Ω) andyou should use only one resistance.

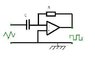
So, I know it's this one: (attached)
But I have to find what resistance to use.

$$\ V_{exit}= \frac {4RCV_{max}}{T}$$
I need that $$\ V_{exit}$$ (that I don't have) to solve for the R !
Any help please ?!

 

[mohlam12]

Never mind... got the answer :)