Circuit with Dependent Current Source

AI Thread Summary
The discussion centers on a homework problem involving nodal analysis with a dependent current source. The user attempted to apply Kirchhoff's Current Law (KCL) at a node but arrived at an incorrect current value of 3*Va instead of the expected -6 A. Participants point out that the ammeter is incorrectly connected in parallel rather than in series, leading to confusion about the circuit setup. They emphasize that if the ammeter were correctly placed, it would directly read the current through the current source without needing calculations. The overall consensus is that the circuit diagram may be flawed, affecting the user's ability to solve the problem correctly.
wk1989
Messages
32
Reaction score
1

Homework Statement


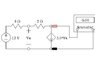
I'm not sure how to solve this question, the method you're supposed to use is nodal analysis.

Homework Equations





The Attempt at a Solution


I tried to use KCL at node A, so I have
Code: 
(12-Va)/8 - 3Va =0

Once I solved Va, the current is 3*Va. However, I'm not getting the right answer which is supposed to be -6 A.

Any help would be appreciated, thanks!
 

Attachments

  • Untitled.jpg
    Untitled.jpg
    9 KB · Views: 515
Physics news on Phys.org
The setup makes no sense. You don't connect ammeters in parallel with circuit elements, you connect them in series.

Are you sure this is how the diagram appears in your book?
 
This was on a list of exercise problems from a university website, but ignoring that, how would you find the current through the current source?
 
wk1989 said:
how would you find the current through the current source?

That is precicely why the setup makes no sense. If the ammeter truly is reading the current through the current source, then you don't need to calculate the current. You just read it! But that ammeter cannot possibly be reading the current through the current source, because it's connected wrong.
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »

Thread 'Rolling without slipping on a curved surface'

Kindly see the attached pdf. My attempt to solve it, is in it. I'm wondering if my solution is right. My idea is this: At any point of time, the ball may be assumed to be at an incline which is at an angle of θ(kindly see both the pics in the pdf file). The value of θ will continuously change and so will the value of friction. I'm not able to figure out, why my solution is wrong, if it is wrong .
View full post »

Similar threads

Single Loop Potential difference -- sign issue
Replies
8
Views
1K
Determine the Thevenin equivalent circuit
Replies
2
Views
2K
Current through an inductor as a function of time
Replies
10
Views
385
Calculation of current in driven series RLC circuit
Replies
8
Views
2K
Mesh Analysis Method for Finding Current in a Circuit with Dependent Source
Replies
5
Views
2K
Find the equivalent resistance of this circuit
Replies
31
Views
4K
Nodal analysis of this circuit with 2 sources and 4 resistors
Replies
12
Views
2K
Kirchoffs Current Law to find voltage?
Replies
16
Views
2K
Current Source in Parallel with Short Circuit
Replies
5
Views
5K
Ohm's Law - Finding Source Voltage
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top