CIRCUITS: Four resistors and a voltage supply (very easy)

[VinnyCee]

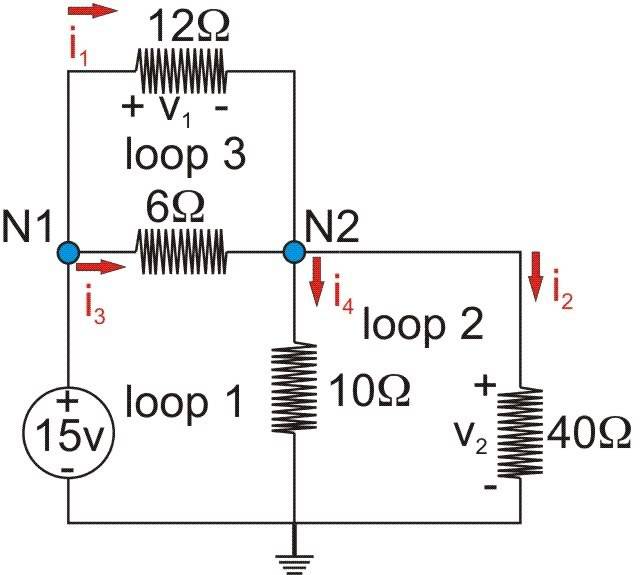
Find v1 and v2 in the circuit shown. Also calculate i1 and i2 and the power dissipated in the 12-ohm and 40-ohm resistors:

My work so far:

i_1\,=\,\frac{N1\,-\,N2}{12\Omega}

i_2\,=\,\frac{N2\,-\,0}{40\Omega}

i_3\,=\,\frac{N1\,-\,N2}{6\Omega}

i_4\,=\,\frac{N2\,-\,0}{10\Omega}

KCL at N2: i_1\,+\,i_3\,=\,i_4\,+\,i_2

KVL for loop 1: 15V\,+\,i_3(6\Omega)\,+\,i_4(10\Omega)\,=\,0

KVL for loop 2: i_4(10\Omega)\,-\,i_2(40\Omega)\,=\,0

I have no idea where to go from here. These things are so confusing! What would I do to get the i1 and i2?

I know that the voltage at N1 is -15V, but how do I solve the rest?

 

[FrogPad]

You can also loop around the top. You would then have 4 equations and 4 unknowns. Also, your expression:
i_4(10\ohm)\,+\,i_2(40\ohm)\,=\,0

Lets say you are following the direction of the I4 current in your loop. When you come to the 40 ohm resistor the direction of the current is opposite of the direction of the loop. What does that say about the polarities?

Also, what would happen if you combined the 6k and 12k resistor, and the 10 and 40 resistor? What does that look like?

If you know the voltage across the 40ohm resistor, what is the voltage across the 10ohm?

 

[VinnyCee]

KVL at loop 3: i_1\,(12\Omega)\,-\,i_3\,(6\Omega)\,=\,0

Which makes a 4 X 4 matrix starting with the KCL and ending with the KVL3 equation:

\left[\begin{array}{ccccc}<br /> 1 &amp; -1 &amp; 1 &amp; -1 &amp; 0 \\<br /> 0 &amp; 0 &amp; 6 &amp; 10 &amp; -15 \\<br /> 0 &amp; -40 &amp; 0 &amp; 10 &amp; 0 \\<br /> 12 &amp; 0 &amp; -1 &amp; 0 &amp; 0<br /> \end{array}\right]

This RREF's out to:

i_1\,=\,-.4167\,A

i_2\,=\,-.2500\,A

These signs are flipped though, why?

 

[OlderDan]

KVL for loop 1: 15V\,+\,i_3(6\Omega)\,+\,i_4(10\Omega)\,=\,0

Check signs?

 

[SGT]

The 2 resistors between nodes N1 and N2 are in parallel. You can replace them by their equivalent and use only 3 currents and 2 loops.

 

[junior_J]

i = i1 +i3 = i4
In Loop 1 ,
15 -i3*6 - i4*10 = 0 (im not sure about this , its grounded ?)

In Loop 3,
i1*12 - 6*i3 = 0

In Loop 2
i2*40 - i4 * 10 = 0

That looks wrong to me oh but what the heck ...

 

[OlderDan]

i = i1 +i3 = i4
In Loop 1 ,
15 -i3*6 - i4*10 = 0 (im not sure about this , its grounded ?)

In Loop 3,
i1*12 - 6*i3 = 0

In Loop 2
i2*40 - i4 * 10 = 0

That looks wrong to me oh but what the heck ...

At N2 there are four wires connected. Each of those has a labeled current. KCL at this node involves all four currents. You have not used them all.

The ground does not change the problem. It just establishes one point where we will call the potential zero. All that really matters is potential differences, so you can ignore the ground. (If the circuit showed multiple grounds that would be equivalent to having wires connecting the grounded points together.)

It would be best if you said which way you are going around the loop. For Loop 1 your equation is correct, and I would say you went around clockwise. For Loop 3 your equation is correct, and I would say you went around counterclockwise. For loop 2 your equation is correct, and I would say you went around counterclockwise.

 

[junior_J]

Loops 2 and 3 were confusing (i made guesses but i didnt really choose a direction , infact i thought i was going clockwise for all the loops ) ... can u explain why i got the results that i got for 2 and 3 ... ? or may be explain how u would go about solving loops 2 and 3

 

[junior_J]

hmm ... i guess i1 + i3 = i4 + i2 at node N2

 

[OlderDan]

hmm ... i guess i1 + i3 = i4 + i2 at node N2

That is correct. I will respond to your other question in a few minutes.

 

[OlderDan]

Loops 2 and 3 were confusing (i made guesses but i didnt really choose a direction , infact i thought i was going clockwise for all the loops ) ... can u explain why i got the results that i got for 2 and 3 ... ? or may be explain how u would go about solving loops 2 and 3

When you set up a problem, you guess at the direction of the current in each branch of a circuit. If you guess wrong it does not matter. All that happens is the solution gives you negative currents, which tells you that the current is opposite your guess. The directions in this diagram are reasonable guesses for the four currents.

I would use the CW direction for Loop 1 because I like to have voltage increases when going through a source of emf, and I would start by first going through the source. So I would write

+15V - i3*6Ω - i4*10Ω = 0

This is exactly the same as your equation.

For Loops 2 and 3 there are no sources of emf. Even if there were, it is often best to do all loops in the same direction, but it is not required. In this problem there is nothing even tempting me to change direction, so I will stick with CW. For Loop 3

- i1*12Ω + i3*6Ω = 0

The first term is negative because I am going in the direcion of the assumed current. The second term is positive because I am going against the assumed current.

For Loop 2

- i2*40Ω + i4*10Ω = 0

As for Loop 3, the first term is negative because I am going in the direcion of the assumed current. The second term is positive because I am going against the assumed current.

Combined with the KCL equation, there are now 4 equations for the 4 unknown currents. These can be solved to find each current.

 

[Maxwell]

You know that this entire circuit collapses into one equivalent resistor, right?

 

[junior_J]

got it ! thank u ! and bless u ! :)

one more question how do other folks here draw those nifty little resistors ?? I can't imagine doing that on mspaint ? do they use some kinda physics software package or something ?

 

[OlderDan]

got it ! thank u ! and bless u ! :)

one more question how do other folks here draw those nifty little resistors ?? I can't imagine doing that on mspaint ? do they use some kinda physics software package or something ?

I do not know where those diagrams came from. They are probably from some commercial circuit drawing program.

 

[VinnyCee]

I used CorelDRAW 10 for the diagram. After you have a set of elements made (resistor, CCVS, etc.) it is not that hard to do. The tedious part is making and copying the elements and then marking their values. There is a program called Pspice that will solve circuits like this one.