Hoophy
- 90
- 61
Homework Statement
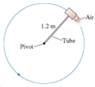
Question: A 600 g steel block rotates on a steel table while attached to a 1.20 m-long hollow tube. Compressed air fed through the tube and ejected from a nozzle on the back of the block exerts a thrust force of 5.01 N perpendicular to the tube. The maximum tension the tube can withstand without breaking is 40.0 N. Assume the coefficient of kinetic friction between steel block and steel table is 0.60.
If the block starts from rest, how many revolutions does it make before the tube breaks?
Homework Equations
My variables and constants:
Steel Block Mass = m = 0.600 kg
Radius = r = 1.2 m
Maximum Tension = T = 40.0 N
Thrust/Tangential Force = F = 5.01 N
g = 9.8 m/s2
Weight = mg
Coefficient of Kinetic Friction = μ = 0.60
Normal Force = N
Friction = z
Centripetal Acceleration = ac
Angular Acceleration = α
Maximum Angular Velocity = ω
Maximum Tangential Velocity = v
Tangential Acceleration = at
The Attempt at a Solution
a) I drew a partial free body diagram showing only the vertically acting forces Normal Force (up, positive y) and Weight (down, negative y)
b) I summed the forces in the vertical axis:
Fvertical: 0 = N - mg
c) I isolated N:
N = mg
d) I drew another partial free body diagram showing only Friction (z), Thrust, and Tension. The situation I used is one in which the Steel Block is directly North of the center-point of the circular path such that Tension points South, Thrust points West, and Friction points East.
I defined my coordinate system as:
1) Positive x is West
2) Positive y is South
e) I summed the forces in the y axis:
Fy: mac = T
ac = T/m
f) I summed the forces in the x axis:
Fx: mat = F - z
mat = F - μmg
at = (F/m) - μg
g) I did circular motion shenanigans:
ac = v2/r = T/m
See (e)
v = sqrt(Tr/m)
ω = v/r
ω = ( sqrt(Tr/m) )/r = ( sqrt[ (40)(1.2)/(0.6) ] )/(1.2) = 7.45356 rad/s
α = at/r
See (f)
α = ( (F/m) - μg )/r = F/(mr) - (μg)/r = (5.01)/( (0.600)(1.2) ) - (0.60)(9.8)/(1.2) = 2.05833 rad/s2
h) More circular motion shenanigans:
Kinematic Equation: ω2 = 2αΔθ
Δθ = ω2/(2α) = (7.45356)2/(2(2.05833)) = 13.4953 rad
i) I computed the number of revolutions:
Δθ/2π = (13.4953)/2π = 2.1478 revs = 2.1 revs
4. A note
2.1 revs is not the correct answer, nor is 2.1478 revs. Also I do not know what the correct answer is...
I don't know where I went wrong.
Thanks for taking the time to read this!
[EDIT] 2.1 revolutions is correct.
Attachments
Last edited: