- #1
Jimbo86
- 9
- 0
Hi,
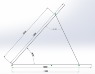
I essentially have a class 2 lever, which holds an unevenly spread load. The lever itself (platform) is however an even weight throughout its length (except for the odd RSJ I've welded in for strength). This is an OLD machine, and hence we're going to build a bigger, stronger and higher capacity machine.
I've done a beam schematic and calculated the required effort to hold the platform with uneven weight in equilibrium. Which I think / hope is right. See below:
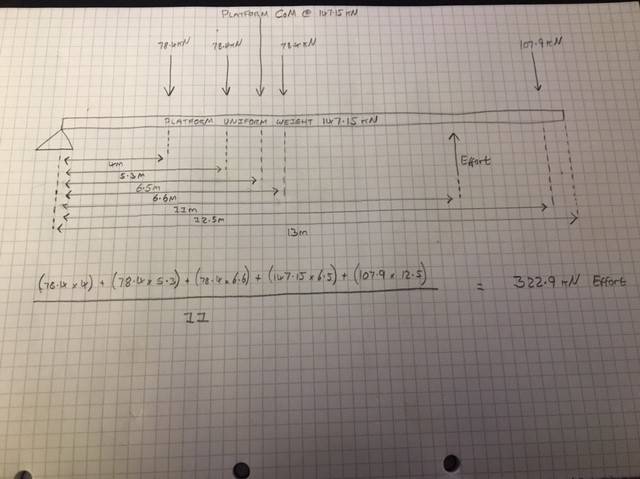
So 11 meters from the fulcrum will be the effort, which I've calculated needs to be 322.9kN for equilibrium.
Now below is the bit I'm slightly unsure of. I need to calculate the effort required to maintain equilibrium at different angles of the lift. And I presume as the angle of the lever increases the required effort reduces as the centre of gravity is essentially being shifted closer to the fulcrum? See below.
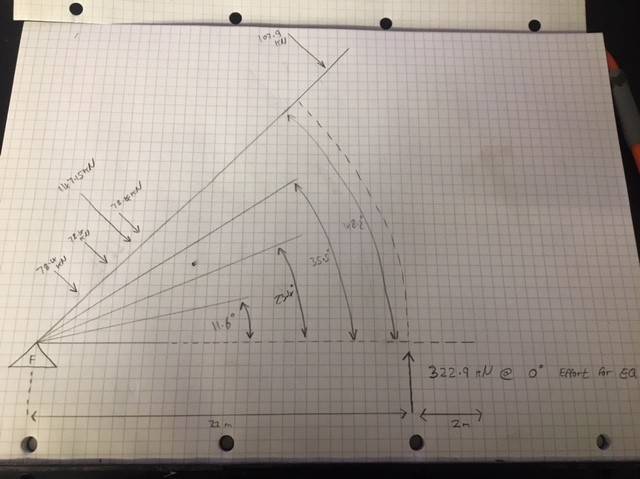
What would be the best method used to calculate this?
Thanks,
Jim
I essentially have a class 2 lever, which holds an unevenly spread load. The lever itself (platform) is however an even weight throughout its length (except for the odd RSJ I've welded in for strength). This is an OLD machine, and hence we're going to build a bigger, stronger and higher capacity machine.
I've done a beam schematic and calculated the required effort to hold the platform with uneven weight in equilibrium. Which I think / hope is right. See below:
So 11 meters from the fulcrum will be the effort, which I've calculated needs to be 322.9kN for equilibrium.
Now below is the bit I'm slightly unsure of. I need to calculate the effort required to maintain equilibrium at different angles of the lift. And I presume as the angle of the lever increases the required effort reduces as the centre of gravity is essentially being shifted closer to the fulcrum? See below.
What would be the best method used to calculate this?
Thanks,
Jim
Attachments
Last edited by a moderator: