Classical mechanics -- Throwing a balloon up into the air....

[Dimani4]

Hi people.

Here the situation. Balloon filled with air I throw in the air. Balloon starts to move upstairs. It slows down and then is starts to fall down to the Earth. I'm interesting only in the movement of upstairs. Here the picture.

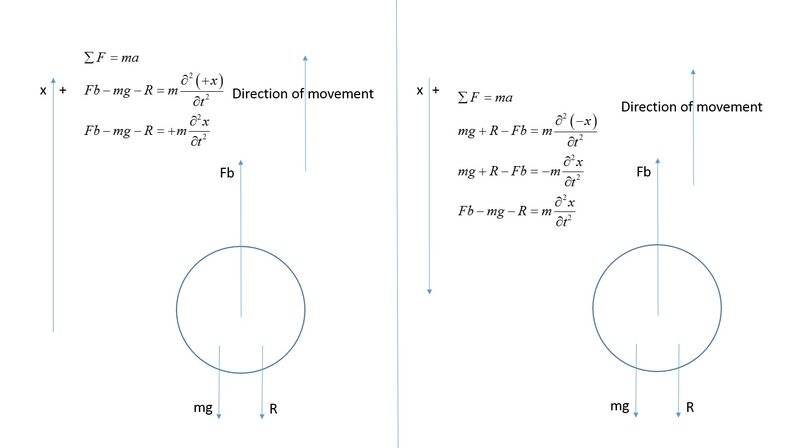
In the first case (left) I choose the direction of positive (x) in the direction of movement. The final equation of motion says to me that the acceleration should be inverse to my chosen positive direction of (x) thus against the direction of movement of my balloon.This is exactly the situation. The acceleration began from maximum at the moment of release of the balloon, and as it moves the acceleration is decreasing till balloon stops and there acceleration equals exactly mg in the direction against the chosen direction of (+x).

In the second case (right) the equation of the forces exactly the same as previous case (left) in spite we have chosen positive x direction against the movement direction. So here if I look at my acceleration direction according the equation I got I see the acceleration should be against the direction of x I have chosen. But I know it's wrong! I know acceleration should be directed in the direction of positive x direction I have chosen. Where is my mistake?

Here: R-air resistance is proportional to the square root of velocity and Fb- buoyancy force.

Thank you very much.

 

[scottdave]

Why do you have a (-x) inside the derivative? Your acceleration could be in either +x or -x direction, which will be determined by all of the forces. If you do d2(x)/dt2 you instead, then you will find that the sum of the forces is in the +x direction {down}

 

[Dimani4]

Why do you have a (-x) inside the derivative? Your acceleration could be in either +x or -x direction, which will be determined by all of the forces. If you do d2(x)/dt2 you instead, then you will find that the sum of the forces is in the +x direction {down}

I wrote it because the direction of movement against the chosen X direction thus I move in -X axis. I may choose the direction of X as I want. Isn't it?

 

[scottdave]

You pick a direction to be positive. You then assign all vectors and sign them with your chosen direction. You are trying to find the 2nd derivative with respect to time of motion in x. If the acceleration comes out a positive number, then it is in the direction of your chosen positive x. If the acceleration comes out negative, then it is in the opposite direction of your chosen +x. By adding the -x inside the derivative, you are actually asking this: What is the acceleration in the negative x direction? A positive number means the acceleration is against your chosen +x. A negative direction means it is with your chosen +x.

. Try it with a simpler problem (like a falling rock) if it helps you understand better.

 

[Dimani4]

You pick a direction to be positive. You then assign all vectors and sign them with your chosen direction. You are trying to find the 2nd derivative with respect to time of motion in x. If the acceleration comes out a positive number, then it is in the direction of your chosen positive x. If the acceleration comes out negative, then it is in the opposite direction of your chosen +x. By adding the -x inside the derivative, you are actually asking this: What is the acceleration in the negative x direction? A positive number means the acceleration is against your chosen +x. A negative direction means it is with your chosen +x.

. Try it with a simpler problem (like a falling rock) if it helps you understand better.

Thank you for your answer. But here the right picture exactly the case you are talking about. Here it turns out that the acceleration according this consideration is turned to be minus meaning that it should be negative to my chosen direction (like Fb is bigger than mg and R ) but this is wrong in that case- acceleration should be in the direction of +X because here acceleration should be in opposite direction of movement.

 

[scottdave]

So if you had put d²(x)/dt² instead of d²(-x)/dt², then you would come up with mg and also R being positive (in the +x direction which is down (and away from direction of motion). This is as you would want it: mg to always point down, and you want R to always be opposite of motion. Also, the buoyant force is negative (which in this convention points upward, as it should).

 

[Dimani4]

So if you had put d²(x)/dt² instead of d²(-x)/dt², then you would come up with mg and also R being positive (in the +x direction which is down (and away from direction of motion). This is as you would want it: mg to always point down, and you want R to always be opposite of motion. Also, the buoyant force is negative (which in this convention points upward, as it should).

Exactly, but it's not possible because such an equation should be for the case when the balloon is moving down. As I understand the equation of motion should remain the same whatever direction of +X or -X I choose. What is important is the direction of movement. But I'm just confusing with the direction of acceleration. If you do the +X axis in the direction of movement everything is ok but if you change the direction of your +X here come the troubles for me.

 

[scottdave]

Off the top of my head, I cannot think of a situation where you would ever have (-x) inside a d/dt or other derivatives. Maybe somebody else can think of one.

Perhaps it may be time to consult your teacher or a tutor - somebody who can sit down with you or go to the blackboard with you, and draw these workings out.
I think there is only so much information and understanding that we can convey, typing messages back and forth. The case which I described does not work for the moving down balloon. Gravity always pulls down. Buoyancy is always up. But the air resistance direction will be opposite the direction of motion. So if your positive reference is down, you have gravity positive, buoyancy negative, and for a falling balloon the air resistance is also negative.

 

[Dimani4]

Off the top of my head, I cannot think of a situation where you would ever have (-x) inside a d/dt or other derivatives. Maybe somebody else can think of one.

Perhaps it may be time to consult your teacher or a tutor - somebody who can sit down with you or go to the blackboard with you, and draw these workings out.
I think there is only so much information and understanding that we can convey, typing messages back and forth. The case which I described does not work for the moving down balloon. Gravity always pulls down. Buoyancy is always up. But the air resistance direction will be opposite the direction of motion. So if your positive reference is down, you have gravity positive, buoyancy negative, and for a falling balloon the air resistance is also negative.

I'm working on this. When I'll get the answer I'll tell you.

 

[scottdave]

I'm working on this. When I'll get the answer I'll tell you.

Great! Keep me posted. Take care.

 

[scottdave]

I just realized, that I wanted to ask you something about the air resistance R. In the beginning, you stated that it is proportional to the square root of velocity. Everything that I have ever seen states that air resistance is some function of velocity^2. Here is one example. http://hyperphysics.phy-astr.gsu.edu/hbase/airfri2.html#c2

 

[Dimani4]

I just realized, that I wanted to ask you something about the air resistance R. In the beginning, you stated that it is proportional to the square root of velocity. Everything that I have ever seen states that air resistance is some function of velocity^2. Here is one example. http://hyperphysics.phy-astr.gsu.edu/hbase/airfri2.html#c2

Yes man, you are absolutely right. Sorry I have confused between square and square root.