rwooduk
- 757
- 59
spent 3 hours on this, getting nowhere
find the change in transition temperature, given: P1,P2,T1,ΔH,density (mixed so gives d1 of metal 1 and d2 of metal 2,atomic weight
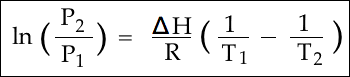
Tried solving for T1 then for ΔT simply saying ΔT = (T1 - T2) , but its clearly not correct and i haven't made use of the densities or the atomic number the question gives.
So then i approximated the problem fromt he original clausius clapeyron eqn to
ΔP/ΔT = ΔH / (TΔV)
but then to find ΔT, which i assume is the change in transition temperature, i need ΔV
so i did density = m/v , PiVi = nRTi to give density = PM / RTi where M is the molar volume
but the density would change with the pressure, so how am i supposed to use the initial density, and there's two densities not one for the compound??
I guess what I'm asking is how do i find ΔV given the above data? why have i been given the two densities of the compound when the densities are going to change with pressure?
Ive spent 3 hours on this question, looked for similar examples on the internet, there are NONE. General questions ask for T2 or P2, none ask for the change in transition temperature.
Please help, erghhhhh, i better get on with my maths now
find the change in transition temperature, given: P1,P2,T1,ΔH,density (mixed so gives d1 of metal 1 and d2 of metal 2,atomic weight
Tried solving for T1 then for ΔT simply saying ΔT = (T1 - T2) , but its clearly not correct and i haven't made use of the densities or the atomic number the question gives.
So then i approximated the problem fromt he original clausius clapeyron eqn to
ΔP/ΔT = ΔH / (TΔV)
but then to find ΔT, which i assume is the change in transition temperature, i need ΔV
so i did density = m/v , PiVi = nRTi to give density = PM / RTi where M is the molar volume
but the density would change with the pressure, so how am i supposed to use the initial density, and there's two densities not one for the compound??
I guess what I'm asking is how do i find ΔV given the above data? why have i been given the two densities of the compound when the densities are going to change with pressure?
Ive spent 3 hours on this question, looked for similar examples on the internet, there are NONE. General questions ask for T2 or P2, none ask for the change in transition temperature.
Please help, erghhhhh, i better get on with my maths now