Closed Wire Loop: Induced Current & Dissipated Energy

[pat666]

Homework Statement

5 A closed wire loop in the form of a square of side 4.0 cm is mounted with its plane horizontal. The loop has a resistance of 2.0 x 10-3Ω, and negligible self-inductance. The loop is situated in a magnetic field of 0.70 T, directed vertically downwards. When the field is switched off, it decreases to zero at a uniform rate on 0.80 s. What is:
a) the current induced in the loop,
b) the energy dissipated in the loop during the change in the magnetic field?
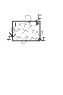
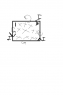
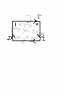
c) Show on a diagram, justifying your statement, the direction of the induced current.

Homework Equations

a) can someone please check this...
\phi=BA
\phi=1.12*10^-3Wb
V=N\Delta\phi/\Deltat
V=1.4*10^-3V
I=V/R
I=0.7A
b) this one I am not sure about
given P=Vi and power is energy over time i derived:
energy =VIt is that energy dissipated or something like total energy?
Energy =7.84*10^-4J
c) see the attachment. sorry about the terrible pic - I don't have a scanner - Conventional current.

Ps. I am not asking anyone to sit down with a calculator and check my work, I just want to know if my procedure is right...\
Thanks

The Attempt at a Solution

 

[ehild]

The method and calculation is correct. Check the direction of current. It must result in a magnetic field inside the loop which has the same direction as the original one, according to Lenz's law "An induced current is always in such a direction as to oppose the motion or change causing it".

 

[pat666]

Thanks ehild, didn't bother reading len's law from the text but I did reach that conclusion.
The only way I get a different direction is if I use electron flow instead of conventional current??
Is this what I should have (still using conventional current)?

 

[ehild]

The only way I get a different direction is if I use electron flow instead of conventional current??
Is this what I should have (still using conventional current)?

Use conventional current. And the direction of the conventional current is opposite to that in the figure.

The magnetic field points downward. When its magnitude decreases, the induced current will produce a magnetic field which direction is the same as that of the original one. Check.

ehild

 

[pat666]

I agree with what you said there (opposite reaction) but that's what I drew in Figure 1 isn't it? Or is my induced current right in figure 1 but my actual current wrong -
looking like

 

[ehild]

This last picture is OK. There is only induced current. There is no current without changing magnetic field, as there is no battery or any other source in the loop. You find the direction of magnetic field by the right-hand rule: if your thumb points in the direction of current your curved fingers around the wire show the magnetic field lines: they point in the direction of the fingertips. See the green hand in the figure.

ehild

 

[pat666]

Thanks for your help ehild, I think I was thinking of a very similar question about an inductor and ac source and confused myself a bit. THANKS