Coefficients in the linear combination of a k-form

[Maxi1995]

Hello,
We defined a k-form on a smooth manifold M as a transfromation

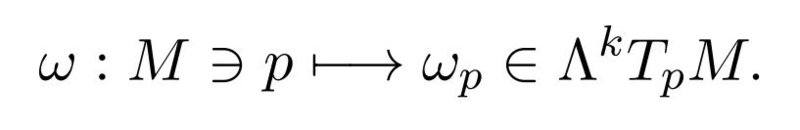
Where the right space is the one of the alternating k-linear forms over the tangent space in p.
If we suppose we know, that we get a basis of this space by using the wedge-product and a basis of the dual space, then we might get for a given form:

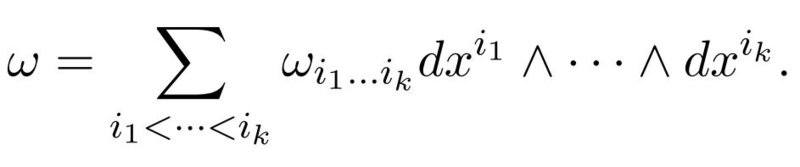
Can someone explain to me what the coefficient in this linear combination is? I know that they are functions and in some cases scalars. But I don't know the cases. According to the definition at the beginning I suppose, that they are funtions for a given p and become scalars if we have argument values of the tangent space. Is this correct?
Greetings
Maxi

 

[fresh_42]

You have $\omega \in \Lambda^k TM$ which is a vector space with basis vectors $dx^{i_1}\wedge \ldots \wedge dx^{i_k}$. Thus the $\omega_{i_1 \ldots i_k}$ are scalars, the coefficients in the linear combination which represents $\omega$ according to this basis.

The evaluation $p \longmapsto \omega_p$ at a certain point affects only the differential forms, resp. the function those forms apply to, not the scalar coefficients.

E.g. if $k=1$ and $\omega = 2dx$ we get $p \longmapsto \omega_p = (f \longmapsto 2df_p)$ or $f(p+v)=f(p)+df_p\cdot v + o(v)=f(p)+\frac{1}{2}\omega_p(f)\cdot v+o(v)$. The coefficient is not affected.

 

[mathwonk]

What fresh says is of course exactly right, but in one special case, you can say more about these coefficients. if you have a set of k one- forms, each written in terms of the n basic one forms dx1,...,dxn, then each of your one - forms needs n coefficients. If you wedge together those k one - forms, you get a k-form expressible in terms of the standard coordinate k-forms, as you have written, with some coefficients you have asked about. Those cofficients in this case are exactly all k by k sub determinants of the n by k matrix of coefficients you began with, the ones expressing the k arbitrary one - forms in terms of the n standard coordinate one-forms. Note there are exactly "n choose k" such k by k subdeterminants.

Indeed if you prove independently that the space of n-forms (at one point) is one dimensional, then one way to define the determinant of a matrix is as the coefficient needed to write the wedge product of its rows in terms of the standard n-form. More abstractly, a linear endomorphism of an n dimensional vector space induces a linear endomorphism of its space of n-linear alternating functions, which must be multiplication by a scalar, which scalar is then defined as the determinant of the original endomorphism.

 

[Maxi1995]

Hello,
thank you for your answer.
@ fresh_42
What is f in your notation? Is it a curve?
I understand what you said about the elements of the basis, thus to say that they are just scalars. But I found in a Wikipedia article (https://en.wikipedia.org/wiki/Differential_form#Differential_calculus) that we might find a linear combination where these factors are smooth functions from $$U \subset \mathbb{R}^n \rightarrow \mathbb{R}$$. Because of this I'm going to add more detail the context in which my question arose.
We defined the outer derivative on $$ \mathbb{R}^n$$ as follows: Let $$w$$ be a k-form on a open set U

Then we define the exteriour derivative by

where

is the (normal) differential of the function $$w_{i_1 \cdots i_k}$$ (Please note that we used here the Einstein notation, so we have a sum over j.).
As you said I expected to be the coefficients scalars, but in this case they are just smooth functions, what puzzled me. Can you explain that to me?
@mathwonk
We had the following:

Where $$V^*$$ is the dual space and j counts the lines and i the columns. What do you mean by subdeterminants?
Best wishes
Maxi

 

[fresh_42]

What is f in your notation? Is it a curve?

A smooth function the differential form $\omega$ applies to, so in general no curve, simply a variable.

The moment you write $d\omega$ you do no longer consider a certain and thus fixed vector in $\Lambda^k$ but investigate what happens by infinitesimal changes of coordinates. You switch from $\vec{v}=v_0\vec{e}_0$ to $\vec{v}(t)=v_0(t)\vec{e}_0$. It is literally the transition from algebra to calculus. Of course now you will have to say in which way these coordinates totter, i.e. what is $t \mapsto v_0(t)$ or in general and local coordinates again, what is $d\omega_{i_1\ldots i_k} = \sum_{j}\dfrac{\partial \omega_{i_1\ldots i_k}}{\partial x^j}dx^j\,.$

If you want to know, why this might confusing you, have a look at the 10 items list at the end of section 1 herein:
https://www.physicsforums.com/insights/journey-manifold-su2mathbbc-part/

I'm not sure whether it will confuses you further or actually be of help, but at least it might serve as a quick reference guide (5 parts):
https://www.physicsforums.com/insights/the-pantheon-of-derivatives-i/

 

[Maxi1995]

Hello,
thank you for your answer, I'm going to read through these pages. I'll give a sign in case of further questions.

 

[Maxi1995]

Hello,
I have another question in this context. Let us say we want to talk about the function as object, thus to say the function itself as element of $$\Lambda ^k V.$$ We derived the coefficients in our proofs by using the smooth k-form itself. We set the coefficients as $$w_{i_1...i_k}=w(e_{i_1},...,e_{i_k})$$. From this and the fact that we made other proofs in $$\Lambda^n V$$ where V was n-dimensional and $$w$$ had the form $$w= f dx_1\wedge...\wedge dx_n$$ with f a smooth function from $$U \subset \mathbb{R}^n \rightarrow \mathbb{R}.$$ I'm still a little bit puzzled, but think this might be caused by vieweing the function as object. Is that right?