Color of light in the Light Clock

[SlowThinker]

In another thread, I came across the question of how the photon's energy and momentum appears in the moving frame. The question is best explained with the standard light clock.
Lets have 2 horizontal mirrors, that is, one above the other. In the rest frame, the photon is set up to be linearly polarized such that its electric field goes in and out of the screen/page.
The points of maximal and minimal intensity are shown as circles in the left part of the picture. Photon is moving up.

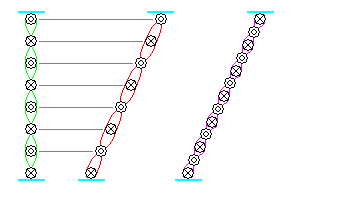
(the green curve is simply a visual cue)
Now there are 2 lines of reasoning that contradict each other:
1. Middle picture
When viewed from a moving frame, the maxima and minima of the electric intensity should be at the same points, that is, at the same height. It means that the color of the photon should be red-shifted, as its wavelength is stretched by the factor $\gamma$.
2. Right picture
The 4-momentum of the photon is, in the rest frame, (E, 0, E, 0). Boosting by $v$ and $\gamma$ in the x-direction, we get
$$E'=\gamma(E-v\cdot 0)=\gamma E$$
$$p_x'=\gamma(0-v\cdot E)=-\gamma v E$$
$$p_y'=p_y=E$$
Since the wavelength is $\lambda'=1/E'=1/(\gamma E)=\lambda/\gamma<\lambda$, the photon appears blue-shifted.

From PeterDonis' comments in another thread, it seems that the second way is correct, but can please someone pinpoint the error in reasoning (1)?

 

[Khashishi]

Photon is redshifted is correct. This is the transverse Doppler effect.
I'm not sure about 2.

I think the problem with 2 is that this approach cannot be applied to a field (which is spread out over space-time). I think you need to use the stress-energy tensor instead of the 4-momentum.

 

[Khashishi]

2 seems to be confounding the momentum of the field with the momentum of a single photon.

 

[bcrowell]

A problem with argument 1 is the following. The wavelength is not just the spatial distance between two events at which the phase differs by $2\pi$. The wavelength is the *shortest* distance between surfaces that differ in phase by $2\pi$, at times that are *simultaneous* in the frame of reference being considered.

 

[PeterDonis]

Boosting by $v$ and $\gamma$ in the x-direction, we get
$$
E'=\gamma(E-v\cdot 0)=\gamma E
$$
$$
p_x'=\gamma(0-v\cdot E)=-\gamma v E
$$
$$
p_y'=p_y=E
$$

First of all, this boost does not correspond to the right-hand picture in your OP. In that picture, the photon is moving to the right; but that means the boost should be in the negative $x$ direction--i.e., the moving frame is moving to the left relative to the stationary frame (the one in the left-hand picture). So the minus signs in your equations above should be plus signs. (As a check, note that this leaves the sign of $E'$ unchanged but makes $p_x'$ positive, which it should be if the photon is moving to the right.)

Second, to know the Doppler effect--i.e., the energy/momentum of a photon as measured by a given observer--it is not sufficient just to know the observer's rest frame. You have to know the motion of the photon relative to the observer in that frame--whether the photon is moving towards, away from, or transverse to the observer (or something in between). In the previous thread you quoted, we were making implicit assumptions about that in order to derive the results we mentioned (that a left-moving photon in a right-moving frame is blueshifted, while a left-moving photon in a left-moving frame is redshifted).

Third, in that previous thread, we were talking about the special case where the boost is in the same or opposite direction as the photon's travel--i.e., the photon is moving either purely towards or purely away from the (implicitly assumed) observer. The case you are posing in this thread involves transverse motion, so you can't just carry over everything we did in the other frame and assume it works.

When viewed from a moving frame, the maxima and minima of the electric intensity should be at the same points

If you're using this model, you can't apply what we did in the other thread at all. I was careful to point out in that thread that if we model light as "photons", in classical SR, we can't think of the light as being waves, so there are no "maxima and minima of intensity". The photons are just particles that move at the speed of light and have energy and momentum, and "frequency" and "wavelength" are just different names for "energy" and "momentum". If you want to study the wave model of light and how it works in SR, that's fine, but then you need to forget everything we said in the other thread and start from scratch, since you are talking about a different model.

 

[SlowThinker]

First of all, this boost does not correspond to the right-hand picture in your OP.

Yes, since I thought the situation is vertically symmetrical, I was careless about the sign of speed. But you're right, of course, that my speed is negative, or I should have used the "+" signs.

Second, to know the Doppler effect--i.e., the energy/momentum of a photon as measured by a given observer--it is not sufficient just to know the observer's rest frame. You have to know the motion of the photon relative to the observer in that frame--whether the photon is moving towards, away from, or transverse to the observer (or something in between).

Now this is strange. Are you saying that the blue-/red-shift cannot be uniquely determined from the horizontal speed $v$? Does it depend on the position of the observer?

Third, in that previous thread, we were talking about the special case where the boost is in the same or opposite direction as the photon's travel--i.e., the photon is moving either purely towards or purely away from the (implicitly assumed) observer. The case you are posing in this thread involves transverse motion, so you can't just carry over everything we did in the other frame and assume it works.

I was ready to analyse the horizontally moving photon once this case is resolved. But it seems easier to discuss this vertical case first. Anyway, that thread includes all 4 directions already.
In the beginning, I didn't realize that the vertical photons are blue-shifted as well in the photon square. When I did, my confusion only grew.

A problem with argument 1 is the following. The wavelength is not just the spatial distance between two events at which the phase differs by $2\pi$. The wavelength is the *shortest* distance between surfaces that differ in phase by $2\pi$, at times that are *simultaneous* in the frame of reference being considered.

I can't really make heads or tails out of this comment (or the rest of Peter's response).
Does the photon's linear polarization change into elliptical in the moving frame? That might move the peaks in intensity to different spots... although only by a constant amount.
Or are you saying that wavelength is only defined for a continuous beam?
Or that the wavelength is actually a vector, that does not need to point in the same direction the photon is moving?
Or... that the reasoning (1) is just plain wrong ?

 

[jartsa]

I don't know if the drawing in post #1 is a snapshot of a photon or many snapshots of a photon at different times.

But why is there not a tilted stack of eight circles, where the distance between circles (wave-length) is small?

EDIT: Oh yes

"When viewed from a moving frame, the maxima and minima of the electric intensity should be at the same points, that is, at the same height"

Hmmm.. well somehow those things do not need to be at the same height.

EDIT: It's not widely known, but vertically length-contracted things length-contract more if you boost them horizontally ... if I understand correctly this: https://www.physicsforums.com/threads/direction-of-length-contraction-in-combined-motion.802815/

 

[PeterDonis]

Are you saying that the blue-/red-shift cannot be uniquely determined from the horizontal speed $v$?

Yes, at least given what it looks like you are trying to do in this thread. Remember that i said, in the other thread (and repeated in post #5 in this thread) that if you are really trying to view light as a wave, and really trying to interpret "frequency" and "wavelength" as properties of a wave, instead of just sloppy ways of saying "energy" and "momentum" for a particle, then you need to forget everything we said in the other thread and start from scratch. If light is a wave, it isn't a particle, classically speaking, and it doesn't have a single position or a single momentum. You can't describe it by a single 4-momentum vector, and you can't derive the real Doppler shift of a real wave by Lorentz transforming a single 4-momentum vector. You need to describe the light wave using more complicated objects that properly capture the spacetime oscillations of the actual wave. In the other thread we were ignoring all that, which is why I was careful to point out that the photons we were talking about in the other thread didn't have a real frequency and wavelength.

 

[PAllen]

A rare circumstance - I think Peter muddied the water unnecessarily.

I think your OP scenario is perfectly well defined, with a unique answer. To clarify any doubt about the set up, note that while there is one receiver in the light clock rest frame, there has to be a row or receivers in frame in which the light clock is moving laterally - each at a current position of the clock's mirror, at rest in the second frame.

Then, with this understanding of the set up, answer (2) is correct, there will be blue shift and the transformed 4-momentum is correct, but a full justification requires fudged quantum mechanics or careful application of Maxwell's equations. Classically, it correctly gives the energy change per 'piece of beam' which could be one cycle, but there is no classical reason to expect this must match frequency change. You can use a fudged quantum argument, with an assumption of preservation of number of photons, or you can see Einstein's 1905 derivation of how the energy change in Doppler, aberration etc. happens to be the same factor as frequency change. Once this result is justified, one way or another, you can rely on 4-momentum transform to correctly describe any Doppler or aberration situation to the extent the geometric optics approximation is true.

Note that this is NOT a transverse Doppler situation where a redshift is expected. That situation results when the beam angle in the emitter rest frame is such as to be transverse between emission event and receiver in the receiver's rest frame. Then the red shift matches the time dilation factor. Here we have a situation where a detector placed so as to receive the beam must such that the emitter is partly approaching them. Classical doppler blueshift wins out over time dilation of emitter frequency, such as to match the transform of the 4-momentum.

To see consistency with Doppler, reference;

https://en.wikipedia.org/wiki/Relativistic_Doppler_effect

and look at the section "Motion in an arbitrary direction". The formula (2) of that section is most readily applicable to this situation, with cosθ_s being zero, due to transverse emission in the emitter rest frame, giving the same result as the transform of 4-momentum. Note, formula (1) of that section is the easy one for transverse Doppler, giving the expected result when cosθ_o is zero.

 

[PeterDonis]

note that while there is one receiver in the light clock rest frame, there has to be a row or receivers in frame in which the light clock is moving laterally - each at a current position of the clock's mirror, at rest in the second frame.

This a good point; for Doppler shift (or energy/momentum of a photon, if we use the particle interpretation) to be well-defined, you have to specify the motion of the receiver.

with this understanding of the set up, answer (2) is correct, there will be blue shift and the transformed 4-momentum is correct

Yes, agreed.

but a full justification requires fudged quantum mechanics or careful application of Maxwell's equations.

Yes, and when you do that, you are no longer treating the photon as a point particle moving at the speed of light, as we were in the previous thread SlowThinker referred to. Which means that you are longer just transforming a single 4-momentum vector from one frame to another (at least, not if you use Maxwell's equations--if you use "fudged quantum mechanics" you might still be able to get away with it, but the word "fudged" is there for a reason ). That was the main point I wanted to emphasize.

Einstein's 1905 derivation of how the energy change in Doppler, aberration etc. happens to be the same factor as frequency change.

I can't remember; was this in his 1905 SR paper, or a different one?

Once this result is justified, one way or another, you can rely on 4-momentum transform to correctly describe any Doppler or aberration situation to the extent the geometric optics approximation is true.

If you specify the 4-velocity of the receiver, as above, yes. (That was another point that wasn't really brought out in the previous thread SlowThinker referred to.)

 

[SlowThinker]

Then, with this understanding of the set up, answer (2) is correct, there will be blue shift and the transformed 4-momentum is correct

So, is one of these true?
1. Electrical and magnetic fields of a photon are an artificial construct, that cannot be directly measured at a given point.
2. When the electric and magnetic fields are transformed correctly, they give the result (2).
I'm trying to figure out where I went wrong...

To clarify any doubt about the set up, note that while there is one receiver in the light clock rest frame, there has to be a row or receivers in frame in which the light clock is moving laterally - each at a current position of the clock's mirror, at rest in the second frame.

Actually this added some doubts
I just need 1 detector in the observer frame to grab the photon out of the clock, don't I?
Or, in the argument (1), to verify the photon's electrical field at a height where zero field is expected.

 

[PeterDonis]

is one of these true?

No, neither one is true.

Re (1), a photon does not have electric and magnetic fields. Saying "photon" in classical physics is a shorthand way of saying "I don't want to bother with all the complications of modeling the actual EM field, so I'm going to assume that I can model all the physics I'm actually interested in by treating light as made up of particles called photons that move at the speed of light and are described by a 4-momentum vector". The term "geometric optics approximation", which PAllen mentioned, is another way of referring to this; in this approximation, there are no electric or magnetic fields, just particles.

Re (2), electric and magnetic fields are not described by a 4-vector, so you can't transform them by transforming a 4-vector. The geometric object that describes the electric and magnetic fields is an antisymmetric 4-tensor; the "time-space" components in a given frame are the electric field in that frame, and the "space-space" components are the magnetic field. So to properly transform the fields, you have to transform a tensor.

 

[SlowThinker]

No, neither one is true.

Re (1), a photon does not have electric and magnetic fields.

Pictures like this

are all over the internet... are they wrong?

Re (2), electric and magnetic fields are not described by a 4-vector, so you can't transform them by transforming a 4-vector.

I could transform them as a tensor then, but actually, the points where both E and B fields are zero would be probably zero in all frames... if such points existed. So it looks like they don't exist?

 

[PeterDonis]

Pictures like this

I didn't say light doesn't have electric and magnetic fields. I said a photon doesn't have electric and magnetic fields, and I explained what "photon" means that makes that the case. "Photon" is not the same thing as "light"; a "photon" is a particular model of light that only works in a certain approximation, and in that model there are no electric and magnetic fields. Please go back and re-read my post.

the points where both E and B fields are zero would be probably zero in all frames... if such points existed. So it looks like they don't exist?

Why would you think that? The picture you posted is not wrong; it just isn't a picture of a "photon". Again, please go back and re-read my post.

 

[SlowThinker]

the points where both E and B fields are zero would be probably zero in all frames... if such points existed. So it looks like they don't exist?

Why would you think that?

In the reference frame connected with the light clock, there would be points of E=0, B=0 at heights that are $\lambda$ apart.
Surely such fields transform into E'=0, B'=0 in all reference frames.
So these same spots could be identified in the moving frame as well, by measuring the fields at various heights in the observer reference frame.
Since this is reasoning (1) again, and that gives the incorrect result, it seems that such points of zero fields cannot be verified with experiment, real or thought.

In fact, trying to improve my original argument, I found Fabry-Pérot interferometer, that is 2 thin horizontal mirrors facing each other at distance $\lambda_0/2$, that let's light through when condition $\lambda=\lambda_0\cos\theta$ is met. $\cos\theta$ happens to be $1/\gamma$ in our setup. So, the faster the light clock moves, the smaller $\cos\theta$ gets and the shorter $\lambda$ gets through.
Which confirms the result (2).
I'm sorry to admit that I found the boosting of momentum a bit hand-wavy, but now I'm convinced it's the correct result.

 

[jartsa]

Let's say a device emits identical EM-wave pulses into a cable. Now we inspect those pulses at different positions on the cable. We find that all pulses are identical. It's like pulses don't change at all as they travel.

We can also do a similar experiment with photons.

Right?

My point here is that there's no waving going on in those EM-wave pulses. There can be detected waving happening inside the cable as a non-waving wave is passing some point of the cable.

Right?

 

[PeterDonis]

In the reference frame connected with the light clock, there would be points of E=0, B=0 at heights that are $\lambda$ apart.

More precisely: in the set of events with the same time coordinate $t$ in the rest frame of the light clock, there would be points of E=0, B=0 at heights that are $\lambda$ apart. But at different times in that frame, these points will be at different spatial coordinates, because the wave crests move at the speed of light.

Surely such fields transform into E'=0, B'=0 in all reference frames.

If E=0, B=0 at some event in one frame, yes, E'=0 and B'=0 at that same event in every other frame. But that event's coordinates, including the time coordinate, will be different in different frames.

If you write down the antisymmetric tensor describing the EM field at different events, and transform it from one frame to another, all this is easy to see.

Since this is reasoning (1) again

No, it isn't. Here you are talking about events, i.e., about points in spacetime. But reasoning (1) only talked about points in space; it didn't include time. If you don't include time, of course you'll get wrong answers. The EM field is a field in spacetime, not space.

To put it another way, your reasoning (1) assumed, implicitly, that if points of E=B=0 are at the same height at the same time in one frame, they must also be at the same height at the same time in the other frame. That is false. The Lorentz transformation between frames doesn't change the "height" coordinate of the events, but it does change the time coordinate.

 

[SlowThinker]

Let's say a device emits identical EM-wave pulses into a cable. Now we inspect those pulses at different positions on the cable. We find that all pulses are identical. It's like pulses don't change at all as they travel.

I see.
I was imagining the photon like a standing wave all the way from source to destination, and I'm seeing a time slice of it as I age.

But it's more like a train, never changing its shape as it moves.
Now the comments about "the same time" make sense.

 

[PAllen]

I can't remember; was this in his 1905 SR paper, or a different one?

It's in the electrodynamics part of this 1905 paper. There being no classical basis for any relation between frequency and energy, he gives independent derivation of the factors for Doppler, noting the 'remarkable fact' that they are the same.

 

[jartsa]

Let's say a wave source produces circular waves at some constant frequency. Observer that stays at constant distance from that source must absorb waves at the same rate as they are produced, as the number of waves between the source and the absorber must stay constant.

Now let's say the observer starts revolving around the wave source. The observer will see a small blueshift of waves:
$$f'=\gamma f$$

That blueshift occurs entirely because of time dilation of the observer, as emitter-absorber distance is still staying constant.

Now let's go to the inertial frame that momentarily co-moves with the observer. In this frame the emitter is time dilated and moving towards the observer, and that approaching motion is the reason for the blueshift. Why does the emitter seem to be approaching? Well because its position is altered by aberration or relativistic beaming.