Aleoa
- 128
- 5
- Homework Statement
- Consider a trough of a semicircular cross-section, and an inclined plane in it that leads from a point A to a point B lying lower than A. Prove that wherever point C is chosen on the arc AB, an object will always get from A to B faster along the slopes ACB than along the original slope AB. The change of direction at C does not involve a change in speed. The effects of friction are negligible.
- Relevant Equations
- (There are no relevant equations)
I'm really sorry, but i don't understand how to solve this problem. Can you give me some help ?
This is the picture of the problem:
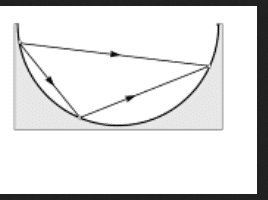
This is the picture of the problem: