Complex currents and voltages - current in a branch

[Rectifier]

The problem
I want to calculate $|I_1|$

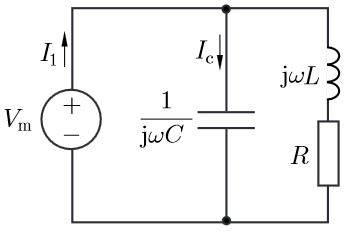
The attempt
$V_m = Z_{total}I_1 \\ I_1 = \frac{V_m}{Z_{total}}$

$Z_{total} = \frac{ \frac{1}{jwC }\cdot (R + jwL) }{\frac{1}{jwC} + R + jwL} \\ \frac{ R + jwL }{1 + jwCR + jwCjwL} \\ \frac{ R + jwL }{1 - w^2LC + jwCR } \\$

$I_1 = \frac{V_m}{Z_{total}} = \frac{V_m}{\frac{ R + jwL }{1 - w^2LC + jwCR }} \\ = \frac{V_m(1 - w^2LC + jwCR)}{R + jwL}$

$I_1 = \frac{V_m(1 - w^2LC + jwCR)}{R + jwL} \\ |I_1| = \frac{|V_m(1 - w^2LC + jwCR)|}{\sqrt{R^2 + (wL)^2}}$

This does not look right since the answer is $\frac{R|V_m|}{R^2 + (wL)^2}$

Please help me.

 

[gneill]

The given answer looks very suspicious since it doesn't include the capacitor impedance in any way. Your result looks okay to me.