- #1
Canadian
- 24
- 0
[SOLVED] Complex Numbers: Eigenvalues and Roots
Below are some problems I am having trouble with, the computer is telling me my answers are wrong. It may be the way I am inputting the numbers but as my final is in a week and a half I would like to be sure.
Thanks,
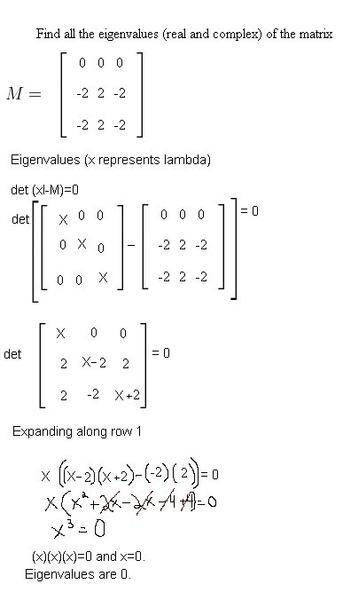

Below are some problems I am having trouble with, the computer is telling me my answers are wrong. It may be the way I am inputting the numbers but as my final is in a week and a half I would like to be sure.
Thanks,