dotNet
- 2
- 0
Hi, I have a complex number and understand that the rectangular form of the number is represented by
s = σ + jω, where σ is the real part and jω is imaginary.
I am having trouble locating them in the number below:
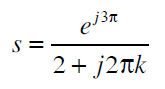
I know that "2" is a real number, and the numerator is imaginary along with j*2*pi*k. Since the numerator is dividing both the elements at the bottom, does this number have a real and imaginary part? (This is where I am a little confused).
My guess would be that σ = 2 and the rest is imaginary.
If I could figure out what parts are real and imaginary, I can go on to find the rectangular form and the polar form.
Thanks
s = σ + jω, where σ is the real part and jω is imaginary.
I am having trouble locating them in the number below:
I know that "2" is a real number, and the numerator is imaginary along with j*2*pi*k. Since the numerator is dividing both the elements at the bottom, does this number have a real and imaginary part? (This is where I am a little confused).
My guess would be that σ = 2 and the rest is imaginary.
If I could figure out what parts are real and imaginary, I can go on to find the rectangular form and the polar form.
Thanks