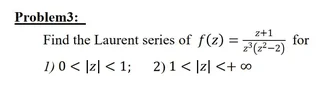##\boxed{
\textbf{Problem 3: Find the Laurent series of } f(z) = \frac{z+1}{z^3(z^2-2)} \text{ for:}
\quad \text{(1) } 0 < |z| < 1 \quad \text{(2) } 1 < |z| < +\infty
}##
**Partial Fraction Decomposition**
We begin with the partial fraction decomposition:
$$f(z) = \frac{z+1}{z^3(z^2-2)} = \frac{A}{z} + \frac{B}{z^2} + \frac{C}{z^3} + \frac{Dz+E}{z^2-2}$$
Multiply both sides by ##z^3(z^2-2)##:
$$z+1 = Az^2(z^2-2) + Bz(z^2-2) + C(z^2-2) + (Dz+E)z^3$$
$$z+1 = A(z^4-2z^2) + B(z^3-2z) + C(z^2-2) + Dz^4 + Ez^3$$
$$z+1 = (A+D)z^4 + (B+E)z^3 + (-2A+C)z^2 - 2Bz - 2C$$
Comparing coefficients:
$$\begin{cases}
z^4: & A + D = 0 \\
z^3: & B + E = 0 \\
z^2: & -2A + C = 0 \\
z^1: & -2B = 1 \\
\text{Constant}: & -2C = 1
\end{cases}$$
Solving:
$$B = -\frac{1}{2}, \quad C = -\frac{1}{2}, \quad -2A - \frac{1}{2} = 0 \Rightarrow A = -\frac{1}{4}$$
$$D = -A = \frac{1}{4}, \quad E = -B = \frac{1}{2}$$
Thus:
$$f(z) = -\frac{1}{4z} - \frac{1}{2z^2} - \frac{1}{2z^3} + \frac{\frac{1}{4}z + \frac{1}{2}}{z^2-2}$$