Vinny_S
- 1
- 0
Member warned that the homework template is required
Here is an example of a problem I am having trouble with. I need to find the i, j, k of A. I have no issues with finding the components for B, but A I just can't wrap my head around when to use cos or sin. Especially here with double projection.
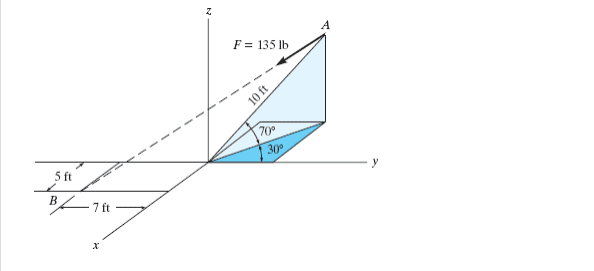
I know that A is :
(-10 cos70 sin30, 10 cos70 cos30, 10 sin70)
Any kind of an explanation regarding why I would do cos vs sin and vice versa would be greatly appreciated. I feel like I am missing something really obvious with this. Thank you.
I know that A is :
(-10 cos70 sin30, 10 cos70 cos30, 10 sin70)
Any kind of an explanation regarding why I would do cos vs sin and vice versa would be greatly appreciated. I feel like I am missing something really obvious with this. Thank you.
Last edited by a moderator: